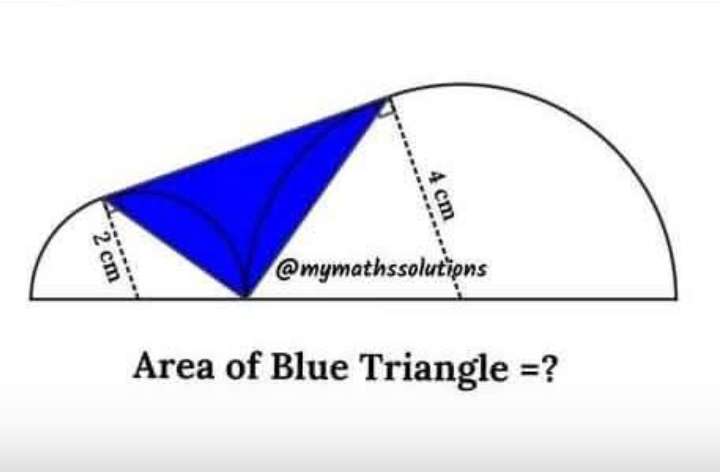
Calculating x, the length that form tangents of the two semi circles.x²+2²=6²x²=36-4x²=32x = √(32) cm.x = 4√(2) cm.Therefore;Area blue is;Area trapezium with two parallel length 2 cm and 4 cm, and he...
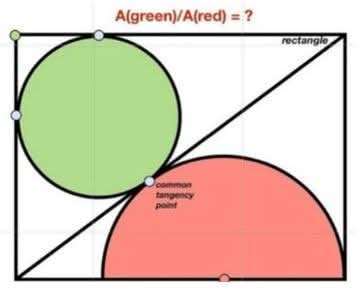
Calculating Area Green ÷ Area Red.Let 2 units be the length of the ascribed rectangle.Let x be the radius of the green inscribed circle.Let y be the radius of the red inscribed half circle.Notice.a =...
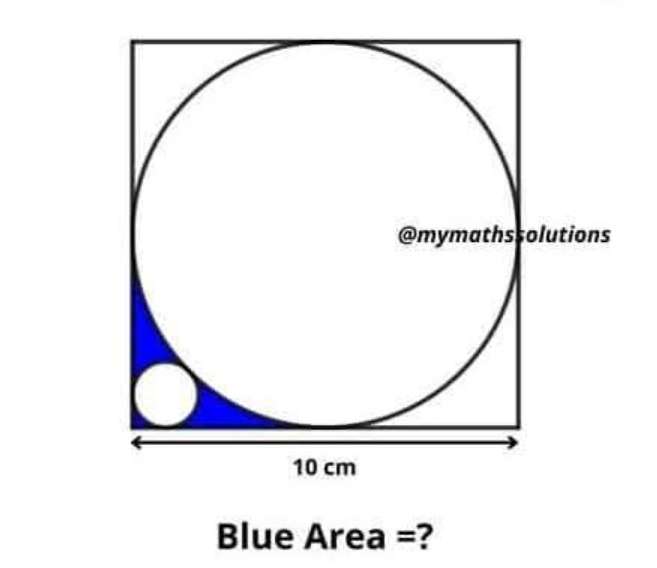
Calculating radius, r of the small inscribed circle.2r² = (5√(2)-5-r)²r = (5√(2)-5)*(√(2)-1)r = (15-10√(2)) cmTherefore blue area is;Area square with side 5 cm - Area quarter circle with radius 5 cm...
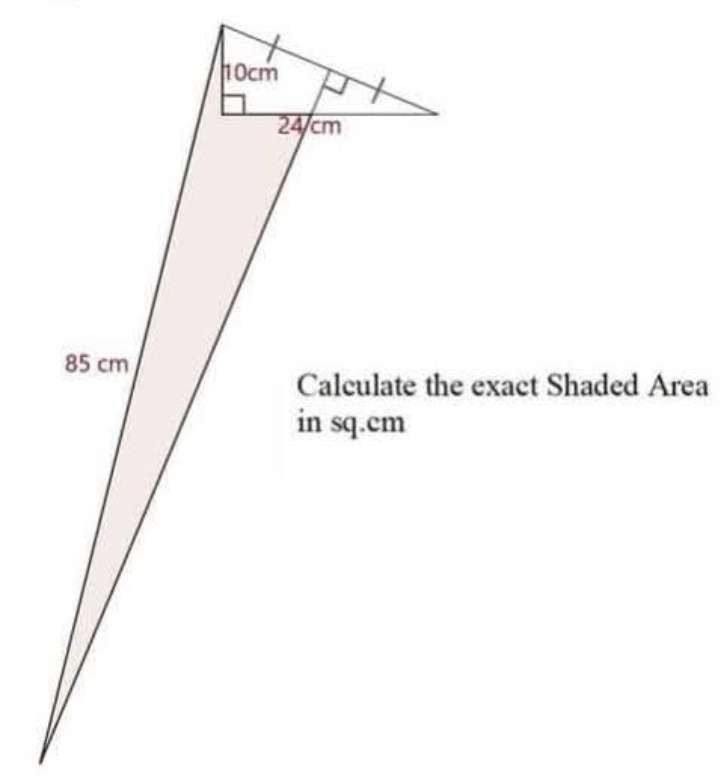
Sir Mike Ambrose is the author of the question.Calculating Shaded Area.Shaded area exactly in cm² is;Area triangle with height 84 cm and base 13 cm - Area triangle with height 10 cm and base 24 cm +...
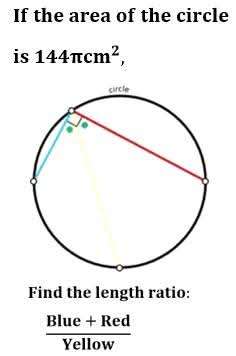
Calculating (length Blue + length red)/(length yellow).Let r be the radius of the circle.Calculating r.πr² = 144πr² = 144r = 12 cm.a = 2ra = 24 cm.a is the diameter of the circle.Let b be the blue le...
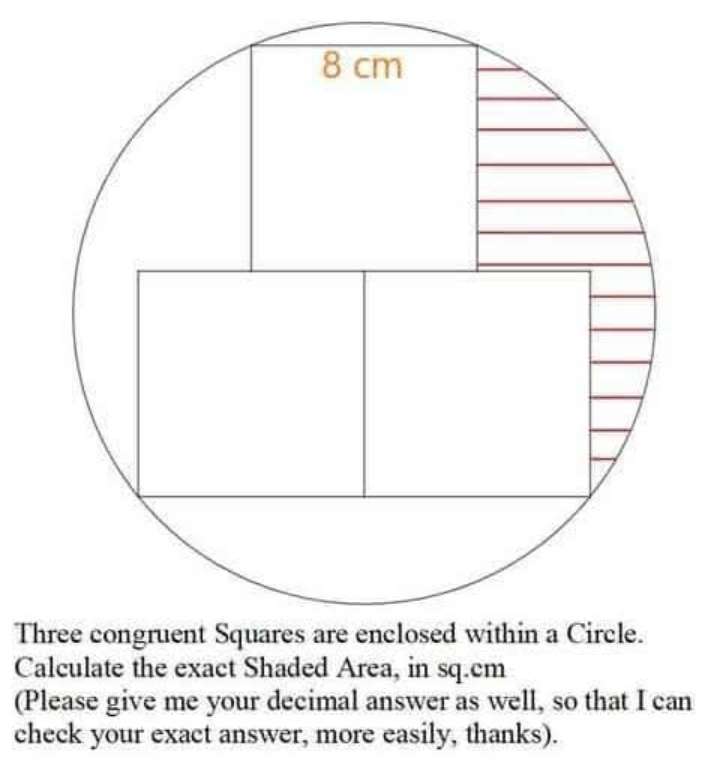
Sir Mike Ambrose is the author of the question.Calculating r, radius of the circle.Radius of the circle, r is;r² = (8+(3/2))²+4²r² = (19/2)²+16r² = ¼(425)r = ½(5√(17)) cmTherefore;Area shaded, exactl...
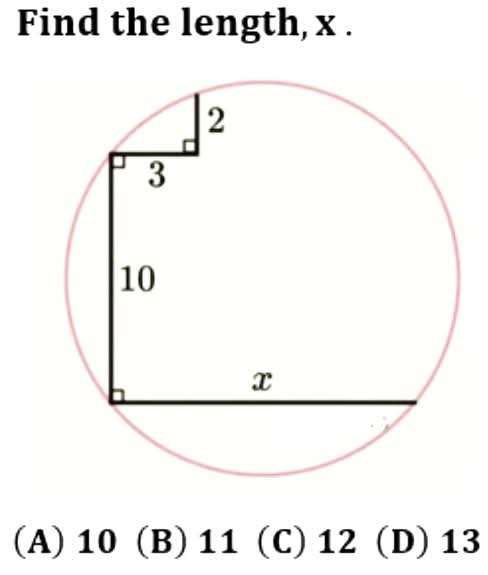
Calculating length x.12*2 = 3(x-3)24 = 3(x-3)24 = 3x-933 = 3xx = 11 units.

Sir Mike Ambrose is the author of the question.
Calculating Area Orange ÷ Area Quadrilateral ABCD Exactly.
Area Orange (trapezoid) is;
Area trapezoid with parallel sides ⅔ units and ½ units,...

Sir Mike Ambrose is the author of the question.
Calculating Exact Area Blue.
Let the small inscribed square side length be x.
The big inscribed square side length will be 2x.
Calculating...

Calculating r, radius of the half circle.
a = 2r units.
a is the diameter of the half circle.
b = ½(2r-4)
b = (r-2) units.
c²+(r-2)² = (4√(3))²
c²+r²-4r+4 = 48
c² = 44+4r-r²
c = √(44+...