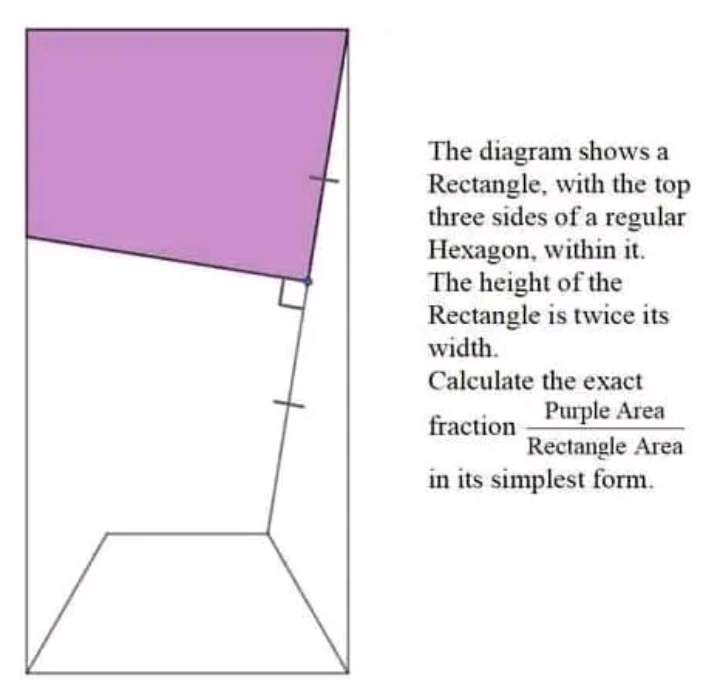
Let the single side length of the three side regular hexagon be 1 unit.
Therefore;
The width of the rectangle is;
2 units.
The length/height of the rectangle is;
4 units.
It impli...
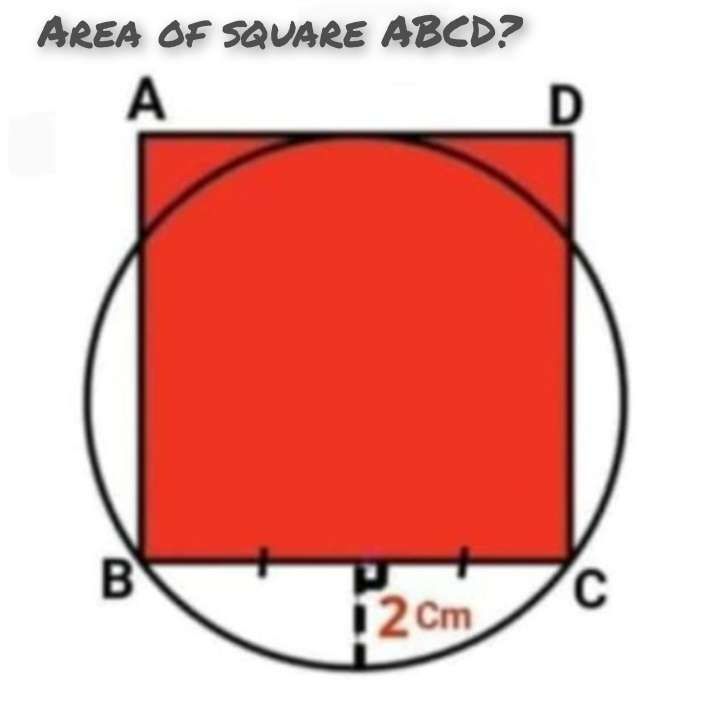
Let the radius of the circle be a.
b = (a-1) cm.
c = (a-2) cm.
It implies, observing Pythagoras rule to get a, radius of the circle.
a² = b²+c²
a² = (a-1)²+(a-2)²
a² = a²-2a+1+a²-4a+4...
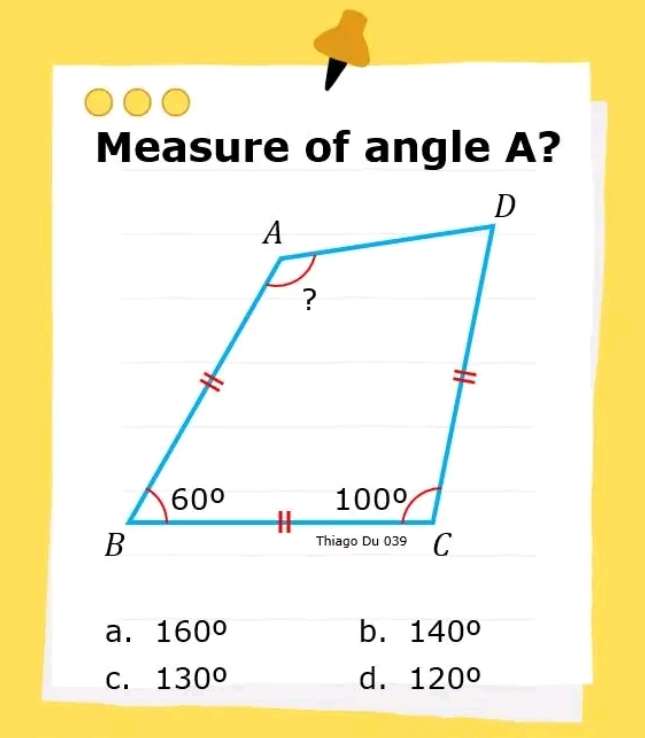
Let the three equal lengths of the quadrilateral be 1 unit each.
Therefore;
a² = 1²+1²-2cos100
a = 1.5320888862 units.
a is BD.
b = 60-½(180-100)
b = 60-40
b = 20°
b is angle ABD....
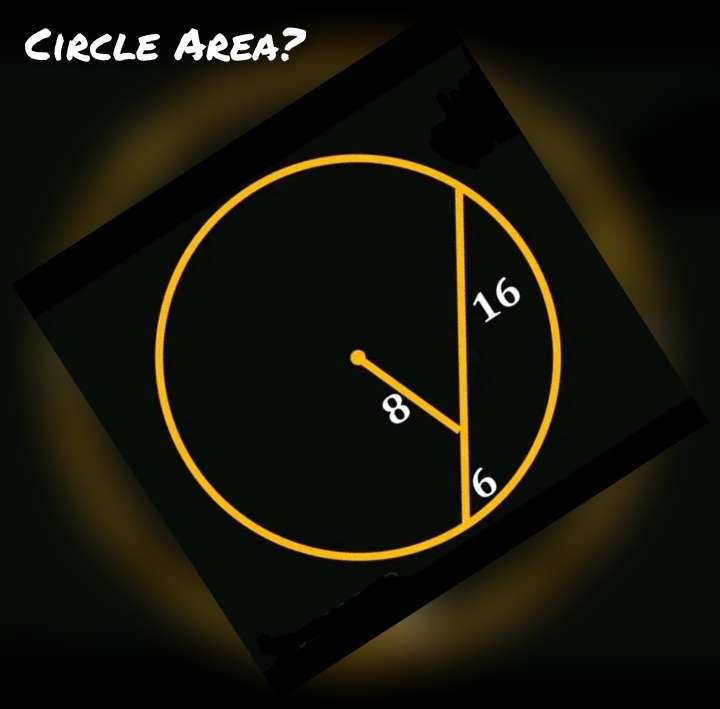
Calculating Area of the Circle.
Let a be the radius of the circle.
Calculating a.
a² = 8²+6²-2*8*6(-cosb)
a² = 100+96cosb --- (1).
a² = 8²+16²-2*8*16cosb
a² = 320-256cosb --- (2).
Eq...
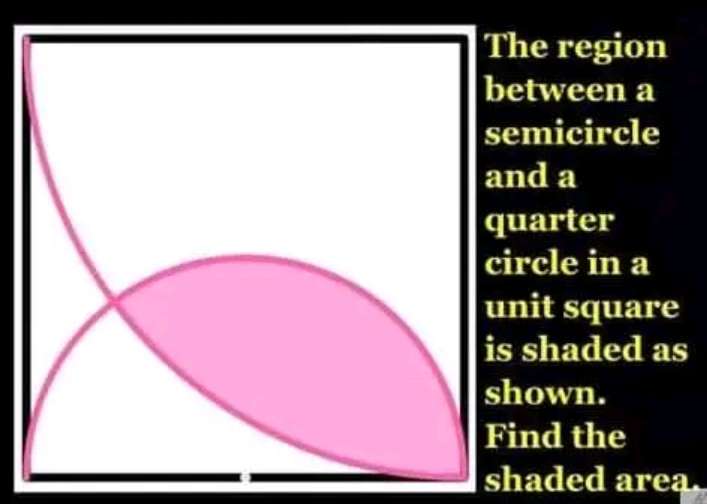
Shaded Area is;
Area sector with radius 1 unit and angle 2atan(½)° - Area triangle with two lengths 1 unit each and angle 2atan(½)°, the angle they form + Area sector with radius ½ units and ang...

Area triangle ABC is;
½(3*(36/5))
= (54/5) square units.
Calculating Area Yellow.
The point coordinates are;
((54/23), (36/23)) (3, 2) ((3/2), (18/5))
Therefore Area Yellow is;
= (39/4...

Area Triangle Blue (S2) is;
½(12)
= 6 square units.
Area Triangle Yellow (S1) is;
½(1.4)sin(atan(4/3))
= (14/25) square units.
Therefore;
S1/S2
= (14/25)/6
= 7/75
Sir Mike Ambrose is the author of the question.
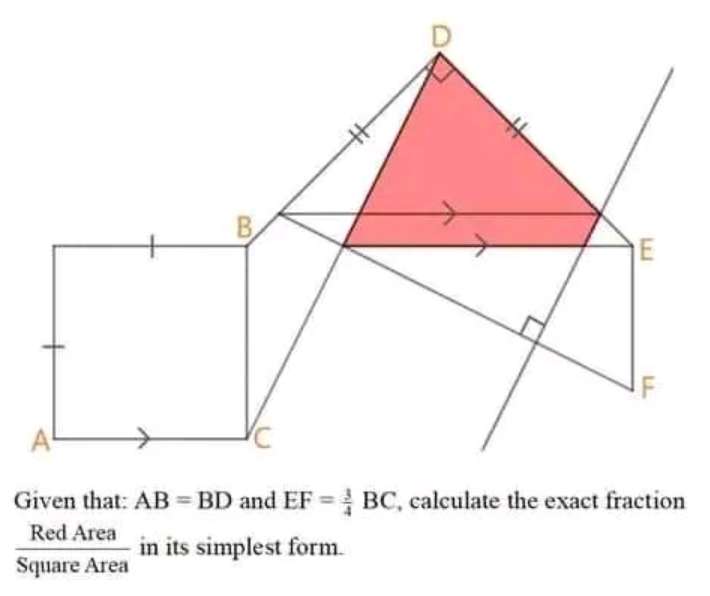
Let the single side length of the square be 2 units.
Therefore;
Area square is;
2*2
= 4 square units.
Area red is;
Area triangle with...
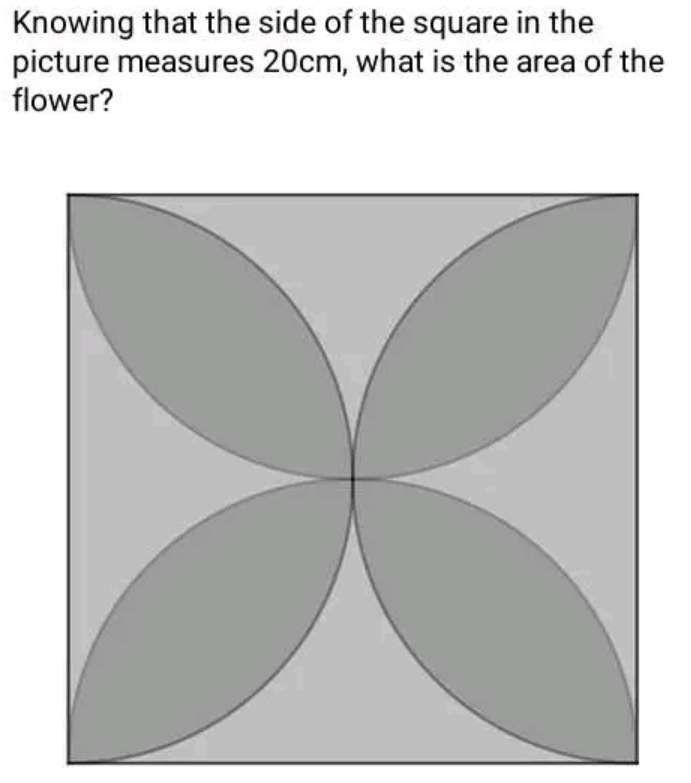
The area of the flower is;
8(area quarter circle with radius 10 cm - area of triangle with height and base, 10 cm respectively)
= 8(¼(100π)-½(100))
= 8(25π - 50) cm²
= 200(π-2) cm²

Let the single side length of the regular hexagon be 1 unit.
Therefore;
Area Regular Hexagon is;
(6*1)/(4tan(180/6))
= ½(3√(3)) square units.
Area Blue/Shaded is;
2(area triangle...