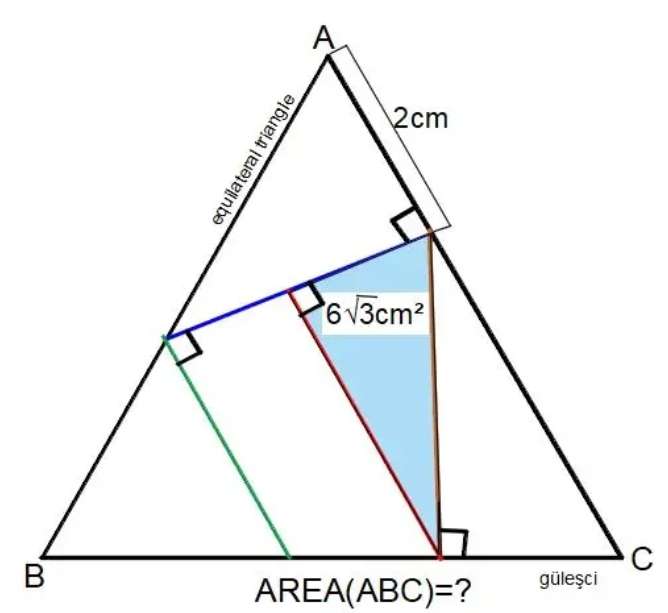
Mathematics Question and Solution
tan60 = a/2
a = 2√(3) cm.
b² = 2²+(2√(3))²
b² = 16
b = 4 cm.
Let the side length of the ascribed regular triangle (equilateral triangle) be x.
c = (x-2) cm.
d = ½(x-2) cm.
e = (x-4) cm.
f = x-(x-4)-½(x-2)
f = ½(2x-2x+8-x+2)
f = ½(10-x) cm.
sin60 = g/½(10-x)
g = ¼(10-x)√(3) cm.
cos60 = h/½(10-x)
h = ¼(10-x) cm.
j = 2√(3)-¼(10-x)√(3)
j = ¼(8√(3)-10√(3)+√(3)x)
j = ¼(√(3)x-2√(3)) cm.
sin60 = k/(x-2)
k = ½(√(3)x-2√(3)) cm.
It implies;
½*½(√(3)x-2√(3))*¼(√(3)x-2√(3))sin60 = 6√(3)
(√(3)x-2√(3))(√(3)x-2√(3))√(3) = 192√(3)
(√(3)x-2√(3))² = 192
3x²-12x+12 = 192
x²-4x+4 = 64
x²-4x-60 = 0
Resolving the above quadratic equation via factorization approach to get x (side length of the regular triangle).
x²-4x-60 = 0
x²-10x+6x-60 = 0
x(x-10)+6(x-10) = 0
(x-10)(x+6) = 0
It implies;
x ≠ -6
x = 10 cm.
Again, x is the side length of the regular triangle (equilateral triangle).
Therefore, area equilateral triangle is;
Area triangle with height 10 cm and base 10sin60 cm.
= ½*10*10sin60
= 25√(3) cm²
= 43.3012701892 cm²