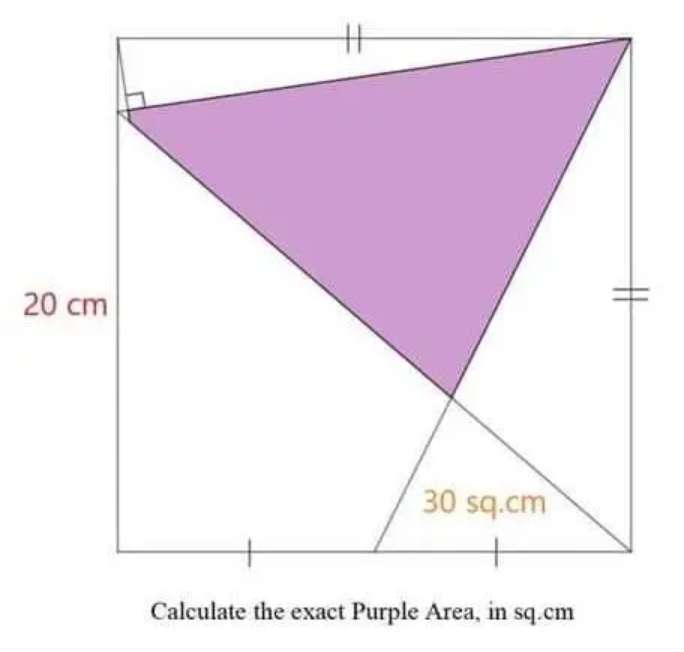
Sir Mike Ambrose is the author of the question.
Area purple exactly in square cm decimal form is;
Area triangle with side 17.1220111351 cm and 15.6524758425 cm, and angle 75.963756532° - Area t...
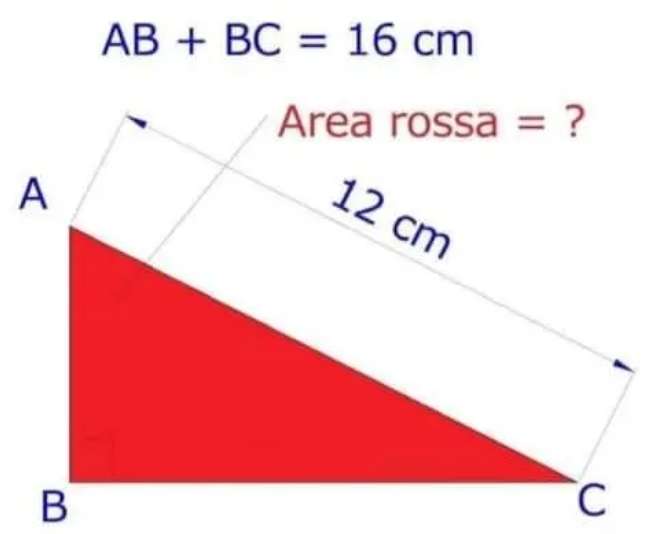
(16-x)²+x² = 12²
256-32x+x²+x² = 144
2x²-32x+112 = 0
x²-16x+56 = 0
(x-8)² = -56+(64)
x = 8±√(8)
x = (8-√(8)) cm.
x = 5.1715728753 cm.
y = 16-x
y = 10.8284271247 cm.
Area triangle red...
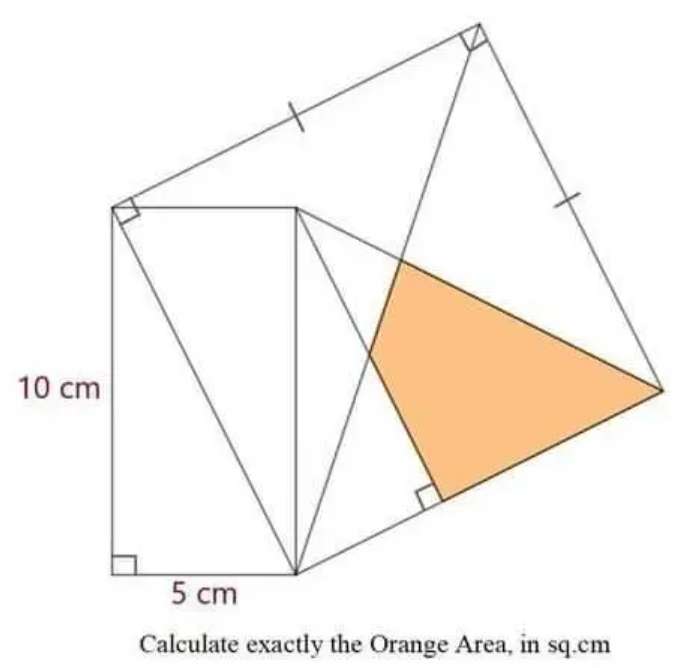
Sir Mike Ambrose is the author of the question.
Area Orange exactly in its simplest decimal cm square form is;
Half area square with side 5√(5) cm - Half area square with side 4.472135955 cm -...
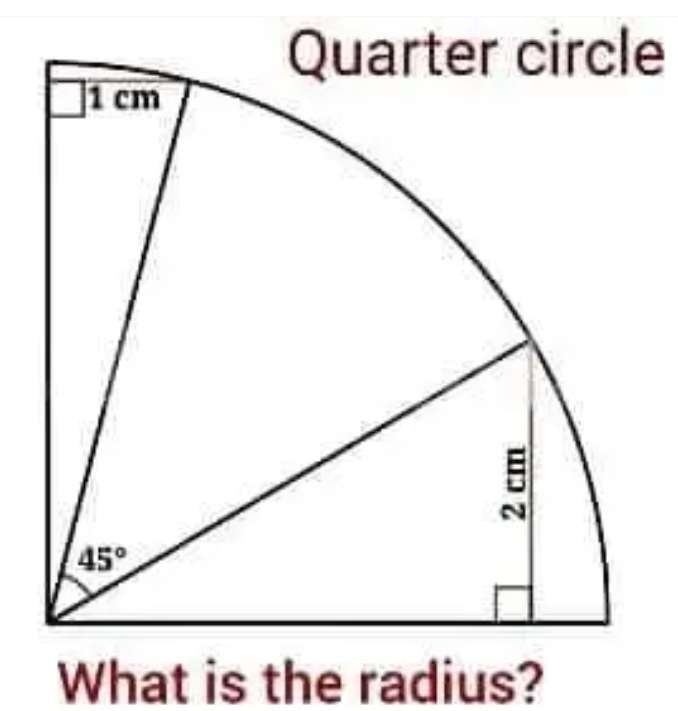
Let a be the radius of the quarter circle.
b = x°
c = (45-x)°
It implies;
sinx = 1/a --- (1).
sin(45-x) = 2/a --- (2).
At (1).
a = 1/sinx --- (3).
Substituting (3) in (2)....
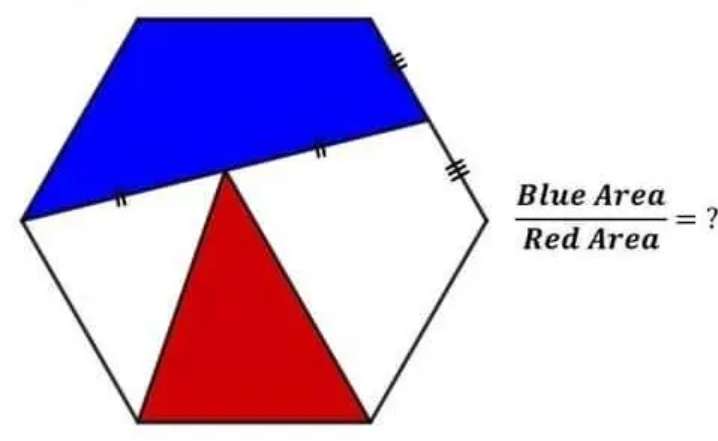
Let the single side length of the equilateral hexagon be 1 unit.
Therefore;
Area blue is;
Area triangle with two sides 1 unit each, and angle 120° + Area triangle with base ½ units and hei...
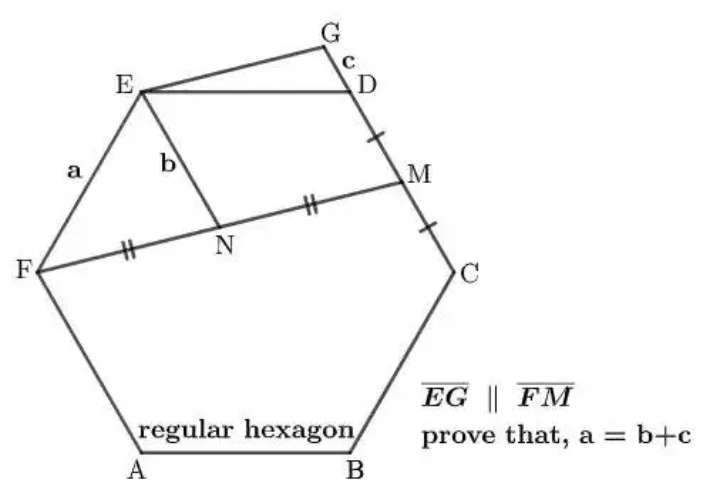
Let a be 1 unit.
d = ⅙*180(6-2)
d = 120°
d is the single interior angle of the regular hexagon.
cos60 = e/1
e = 0.5 units.
f = a+2e
f = 2 units.
f is CF.
g² = 0.5²+2²-2*0.5*2cos60...
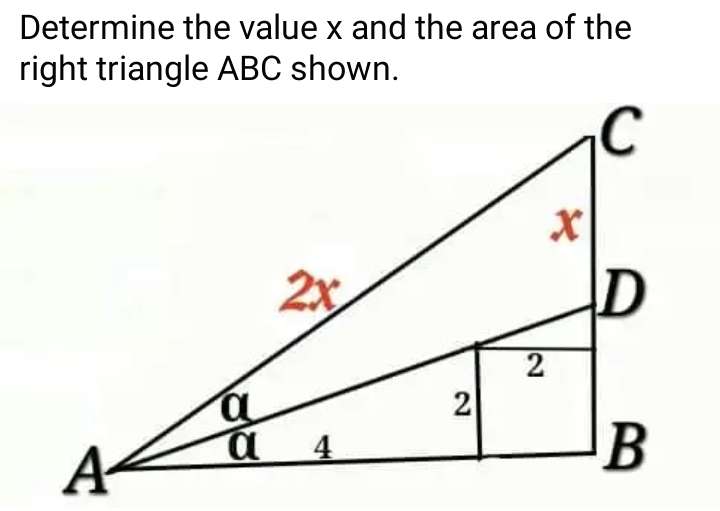
a = x+1+2
a = (x+3) units.
a is BC.
b = 4+2
b = 6 units.
Calculating x.
(2x)² = (x+3)²+6²
4x² = x²+6x+9+36
3x²-6x-45 = 0
x²-2x-15 = 0
x²-5x+3x-15 = 0
x(x-5)+3(x-5) = 0
(x-5)(x+3)...
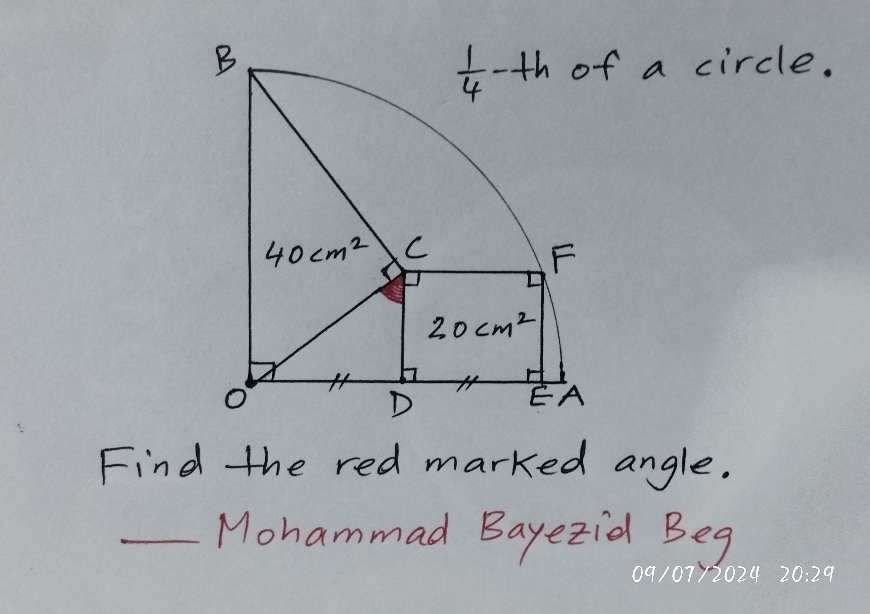
½*a*b = 10
a = (20/b) cm.
a is CD.
b is OD.
b² - 30
(20/b)² - 10
Cross Multiply.
10b² = 12000/b²
10b⁴ = 12000
b⁴ = 1200
b⁴ = 1200
b² = √(1200)
b² = 20√(3)
b = √(20√(3))
b = 5.885...
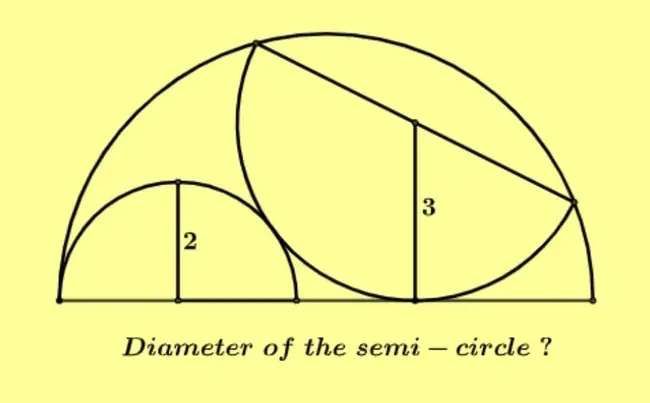
a = 2+3
a = 5 units.
b²+3² = a²
b² = 25-9
b = √(16)
b = 4 units.
Let x be the radius of the ascribed semi circle.
c = (2-(x-4)) units.
c = (6-x) units.
d² = (6-x)²+3²
d² = 36-12x+...
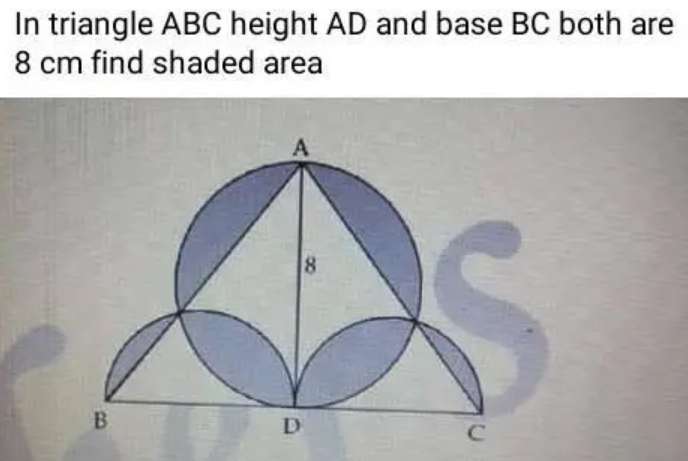
Shaded/Area Blue is;
2(area sector with radius 4 units and angle (180-2atan(½))° - area triangle with two side 4 units respectively, and angle (180-2atan(½))°) + 2(area sector with radius 2 unit...