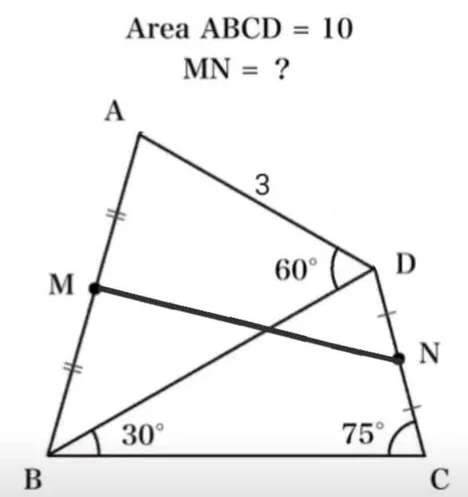
Mathematics Question and Solution
Calculating Length MN.
Let BD = a.
b = 180-30-75
b = 75°
b is angle BDC.
Notice!
Area ABCD = 10 square units.
Calculating a.
It implies
0.5*3*a*sin60 + 0.5*a²sin30 = 10
¼(3√(3)a+¼(a²) = 10
¼(3√(3)a+a²) = 10
a²+3√(3)a-40 = 0
Resolving the above quadratic equation via completing the square approach to get a.
a²+3√(3)a-40 = 0
(a+½(3√(3)))² = 40+(0.5*3√(3))²
(a+½(3√(3)))² = 40+¼(27)
(a+½(3√(3)))² = ¼(160+27)
(a+½(3√(3)))² = ¼(187)
a+½(3√(3)) = √(¼(187))
a = -½(3√(3))±√(187)
It implies;
a ≠ -½(3√(3))-√(187)
a = ½√(187)-½(3√(3))
a = ½(√(187)-3√(3))
a = 4.2393209542 units.
Again, a is BD.
(4.2393209542/sin75) = (c/sin30)
c = 2.1944340025 units.
c is CD.
d = ½(c)
d = 1.0972170013 units.
d is CN = DN.
e² = 3²+4.2393209542²-2*3*4.2393209542cos60
e = 3.7754310072 units.
e is AB.
f = ½(e)
f = 1.8877155036 units.
f is AM = BM.
(3.7754310072/sin60) = (4.2393209542/sing)
g = 76.5158773214°
g is angle BAD
h² = 3²+1.0972170013²-2*3*1.0972170013cos135
h = 3.8547350934 units.
h is AN.
(3.8547350934/sin135) = (1.0972170013/sinj)
j = 11.611341977°
j is angle DAN.
k = g-j
k = 76.5158773214-11.611341977
k = 64.9045353444°
k is angle MAN.
Therefore, the required length, MN is;
Let MN = l.
l² = 3.8547350934²+(0.5*3.7754310072)²-2*3.8547350934*(0.5*3.7754310072)cos64.9045353444
l² = 12.25
l = √(12.25)
l = 3.5 units.
It implies;
Length MN = 3.5 units.