Mathematics Question and Solution
Sir Beg is the author of the question.
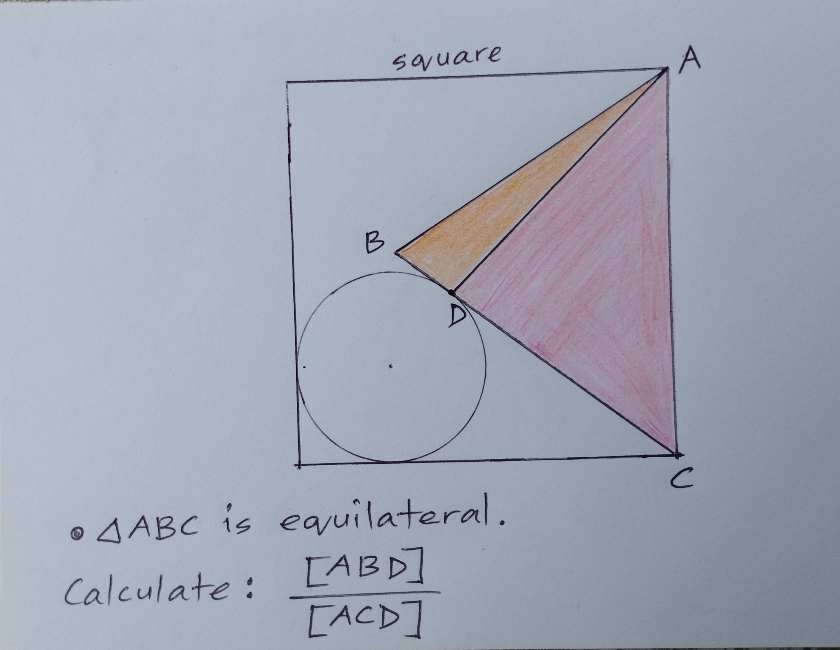
Let the square side length be 1 unit.
1² = 2a²
a = √(1/2)
a = ½√(2) units.
a is AD = CD.
Let the radius of the inscribed circle be b.
Therefore;
c² = 2b²
c = √(2)b cm.
d² = 2(1)²
d = √(2) units.
d is the diagonal of the square.
Calculating b, radius of the inscribed circle.
a+b+c = d
½√(2)+b+√(2)b = √(2)
(1+√(2))b = ½√(2)
b = ½√(2)/(1+√(2))
b = (½√(2)-1)/(-1)
b = ½(2-√(2)) units.
b = 0.2928932188 units.
Again, b is the radius of the inscribed circle.
e = 1- ½√(2)
e = ½(2-√(2)) units.
Therefore;
Area ABD is;
½*½(2-√(2))*½√(2)
= ⅛(2√(2)-2)
= ¼(√(2)-1) square units.
Area ACD is;
½(½√(2))²
= ⅛*2
= ¼ units.
It implies;
Area ABD ÷ Area ACD is;
¼(√(2)-1) ÷ ¼
= (√(2)-1)
= 0.4142135624