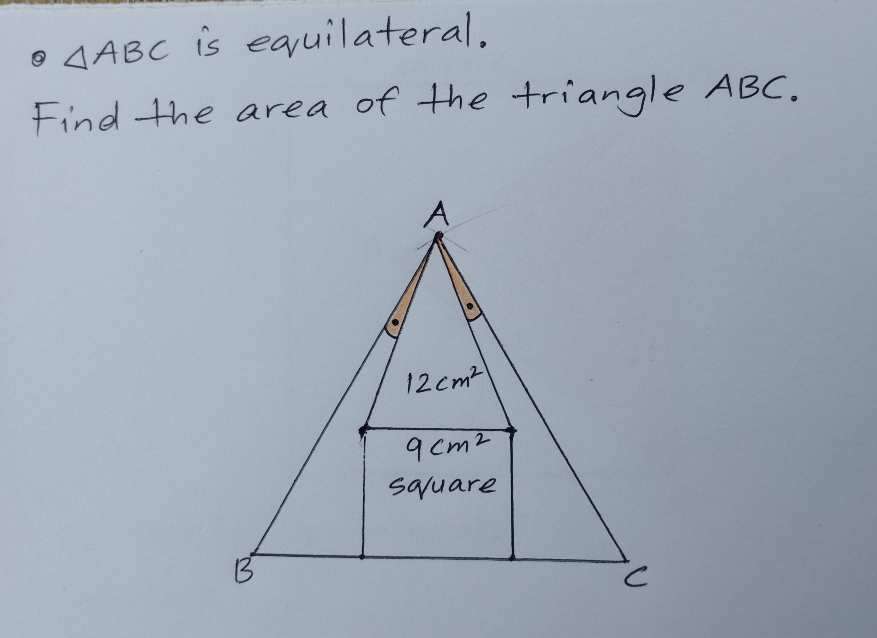
Mathematics Question and Solution
Sir Beg is the author of the question.
Let AB be a cm, the side length of the ascribed equilateral triangle ABC.
b² = 9
b = 3 cm.
b is the side length of the inscribed square and the base of the inscribed triangle.
c²+(½(a))² = a²
c² = a²-¼(a²)
c² = ¼(3a²)
c = ½√(3)a cm.
c is the height of the ascribed equilateral triangle ABC.
d = c-3
d = ½√(3)a-3
d = ½(√(3)a-6) cm.
d is the height of the inscribed triangle.
It implies;
Calculating a, the side length of the ascribed regular triangle ABC.
½*3*d = 12
½*3*½(√(3)a-6) = 12
¼(3√(3)a-18) = 12
3√(3)a-18 = 48
3√(3)a = 66
√(3)a = 22
a = ⅓(22√(3)) cm.
a = 12.7017059222 cm.
Again, a is the side length of the ascribed equilateral triangle ABC.
Therefore, area ascribed equilateral triangle ABC is;
½*a²sin60
= ½*⅓(22√(3))*⅓(22√(3))sin60
= ¼*⅑*3*22*22*√(3)
= ⅓(121√(3)) cm²
= 69.8593825719 cm²