Mathematics Question and Solution
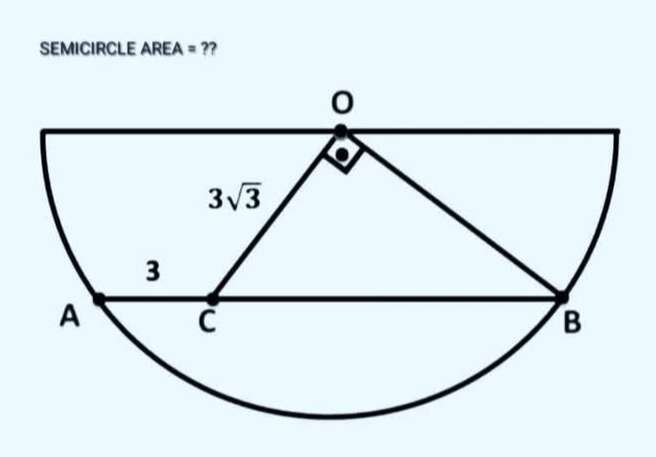
Calculating the area of the ascribed half circle.
Let a be the radius of the circle.
b² = a²+(3√(3))²
b = √(a²+27) units.
c = ½(3+b)
c = ½(3+√(a²+27)) units.
d = c-3
d = ½(3+√(a²+27))-3
d = ½(√(a²+27)-3) units.
e² = (3√(3))²-(½(√(a²+27)-3))²
e² = 27-¼(a²+27-6√(a²+27)+9)
e² = ¼(108-a²-27+6√(a²+27)-9)
e² = ¼(72-a²+6√(a²+27)).
It implies;
Calculating a.
e²+c² = a²
¼(72-a²+6√(a²+27))+(½(3+√(a²+27)))² = a²
¼(72-a²+6√(a²+27))+¼(9+6√(a²+27)+a²+27) = a²
72-a²+6√(a²+27)+36+6√(a²+27)+a² = 4a²
108+12√(a²+27) = 4a²
12²(a²+27) = (4a²-108)²
144a²+3888 = 16a⁴-864a²+ 11664
16a⁴-1008a²+7776 = 0
4a⁴-252a²+1944 = 0
a⁴-63a²+486 = 0
It implies;
a² = 54 or a² = 9
Therefore;
a ≠ √(9) units.
a = √(54) units.
a = 3√(6) units.
a = 7.34846922835 units.
Therefore, area half circle is;
½*πa²
= ½*π(3√(6))²
= ½*54π
= 27π square units.