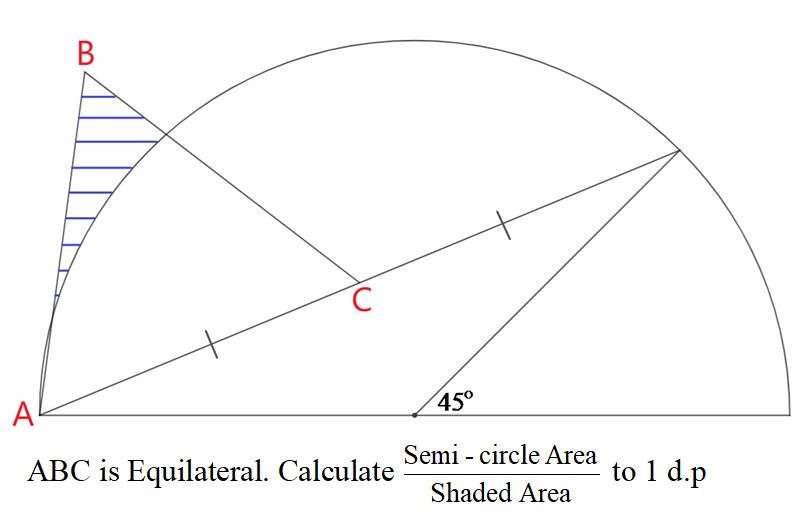
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
Let the radius of the semicircle be 1 unit.
Area Semicircle is;
½*1²*π
0.5π square units.
Calculating AC = AB = BC
sin67.5 = (AC)/1
AC = sin67.5 units.
1=a²+1-2acos82.5
a = 0.26105238444 units.
b = AC - a
b = 0.66282714807 unit.
c = √(0.26105238444²(sin67.5)²-2*0.26105238444sin67.5*cos60)
c= 0.82493683584 units.
d = asin(0.26105238444sin60/0.82493683584)
d = 15.90570135267°
e = 60-d
e = 44.09429864733°
f = 0.650107 unit.
g = 0.57691191774 unit.
h = AC - f
h = 0.27377253251 unit.
i = 33.53107818637°
Area Shaded is;
Area triangle with height 0.66282714807 unit and base 0.27377253251sin60 units - Area sector with radius 1 unit and angle 33.53107818637° + Area triangle with height 1 unit and base sin33.53107818637 units.
= 0.5*0.66282714807*0.27377253251sin60 - 33.53107818637π÷360 + 0.5sin33.53107818637
= 0.07857615932 - 0.29261385805 + 0.27619460884
= 0.06215691011 square units.
It implies;
Area Semicircle ÷ Area Shaded to 1 decimal place is;
(0.5π) ÷ 0.06215691011
= 25.27146738818
≈ 25.3