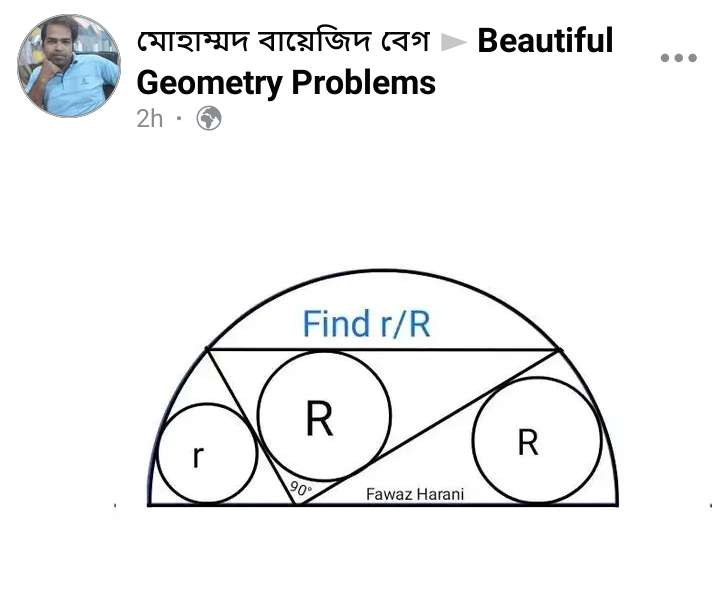
Mathematics Question and Solution
Let the hypotenuse of the inscribed triangle be 10 units.
Calculating the radius of the ascribed half circle.
Let it be a.
2a² = 10²
a² = 50
a = 5√(2) units.
a = 7.07106781187 units.
Calculating r.
(5√(2)-r)² = r²+5²
50-10√(2)r+r² = r²+25
25 = 10√(2)r
5 = 2√(2)r
r = ¼(5√(2)) units.
r = 1.76776695297 units.
Calculating R.
sin30 = a/10
a = 5 units.
cos30 = b/10
b = 5√(3) units.
Where a and b area adjacent base and adjacent height of the inscribed right-angled triangle with hypotenuse 10 units.
It implies;
5R+10R+5√(3)R = 25√(3)
(15+5√(3))R = 25√(3)
(3+√(3))R = 5√(3)
R = 5√(3)/(3+√(3))
R = (15√(3)-15)/(9-3)
R = ⅙(15√(3)-15)
R = ½(5√(3)-5) units.
R = 1.83012701892 units.
Therefore;
r/R is;
¼(5√(2))/½(5√(3)-5)
= ½((5√(2))/(5√(3)-5))
= ½(((25√(6))+(25√(2)))/(75-25))
= ½(25(√(6)+√(2))/50)
= ¼(√(6)+√(2))
Or
r/R in decimal is;
1.76776695297÷1.83012701892
= 0.96592582629