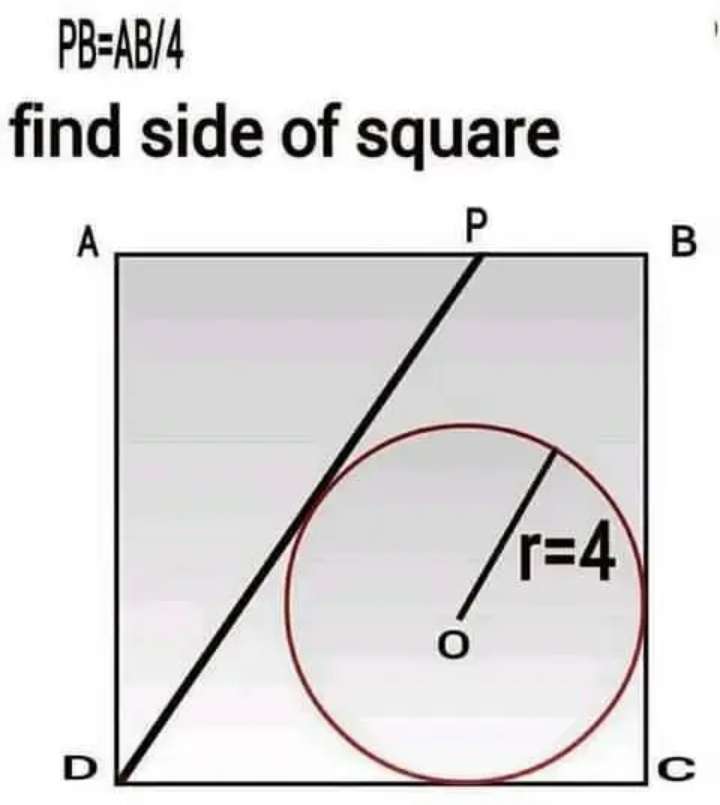
Mathematics Question and Solution
Let the single side length of the square be x.
Therefore;
½(x*(3x/4))+½(4√(x²+(3x/4)²)+½(8x)+½(¼(x)(x-4))=x²
(3x²)/8+2√(x²+(9x²/16))+4x+(x²/8)-(x/2)=x²
3x²+16√(x²+(9x²/16))+32x+x²-4x=8x²
16√(x²+(9x²/16))=4x²-28x
256(x²+(9x²/16))=(4x²-28x)²
256x²+144x²=16x⁴-228x³+784x²
16x⁴-228x³+784x²-400x²=0
16x⁴-228x³+384x²=0
x²-14x+24=0
x²-12x-2x+24=0
x(x-12)-2(x-12)=0
(x-2)(x-12)=0
Therefore;
x≠2
x=12 units.
Therefore, the side length of the square, ABCD is;
12 units.