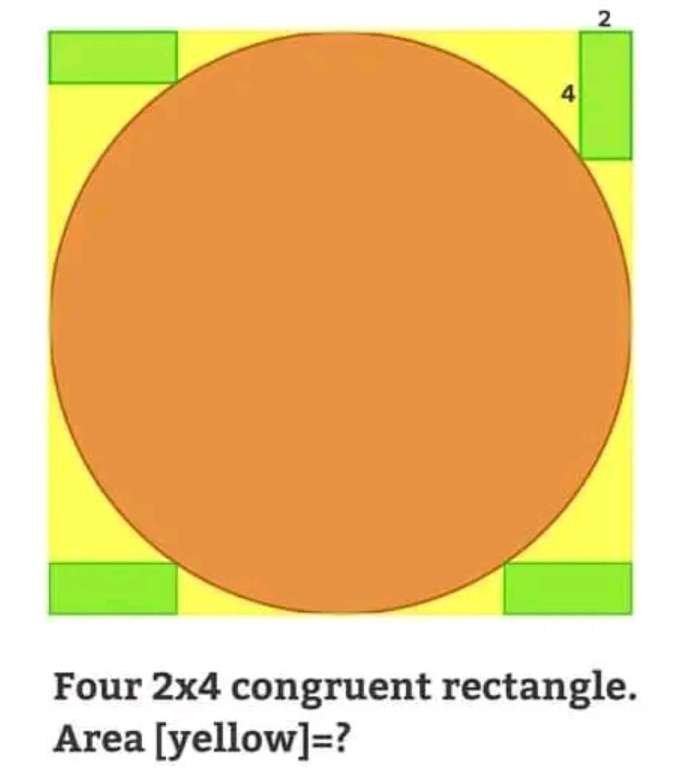
Mathematics Question and Solution
Calculating r, radius of the inscribed circle.
r²=(r-4)²+(r-2)²
r²=r²-8r+16+r²-4r+4
r²-12r+20=0
(r-6)²=-20+36
r = 6±√(16)
r = 6±4
Therefore;
r ≠ 2 units.
r = 10 units.
Therefore, area of the ascribed square is;
(2r)²
= (2*10)² = 20*20
= 400 square units.
It implies;
Yellow region area is;
Area of the ascribed square - 4(area green rectangle) - area inscribed circle with radius 10 units.
= 400 - 4(4*2) - 100π
= 400 - 32 - 100π
= 368 - 100π
= 4(92-25π) square units.
= 53.840734641 square units.