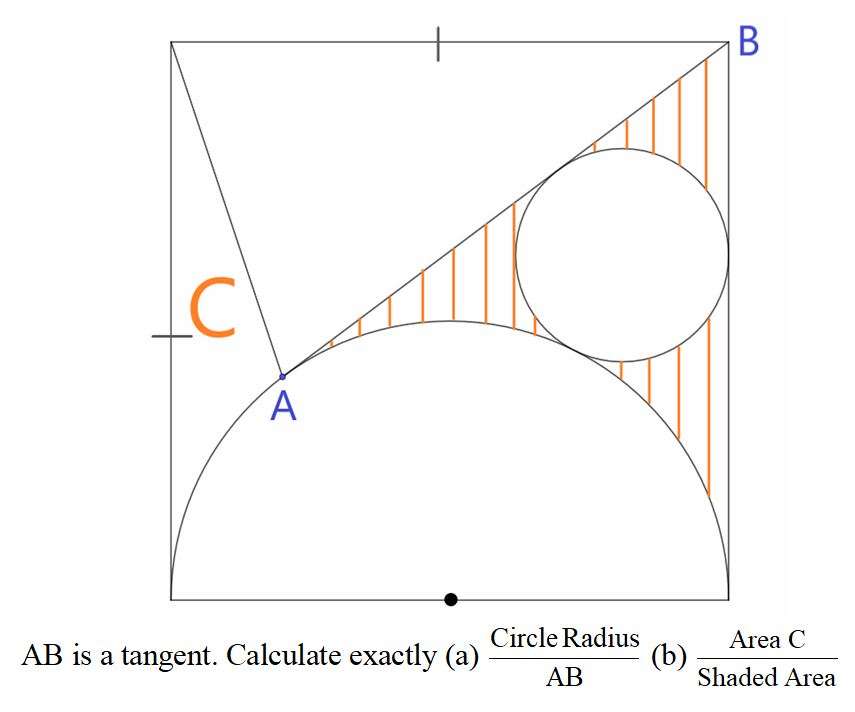
Mathematics Question and Solution
Let AB be 2 units.
a = atan(½)°
b² = 2²+1²
b = √(5) units.
Let r be the radius of the inscribed circle.
Calculating r.
sin(atan½) = r/c
c = r/sin(atan½) units.
It implies;
1+r+(r/sin(atan½)) = √(5)
r+(r/sin(atan½)) = √(5)-1
r+√(5)r = √(5)-1
r = (√(5)-1)/(1+√(5))
r = ½(3-√(5)) units.
(a) Circle Radius ÷ AB exactly is;
½(3-√(5)) ÷ 2
= ¼(3-√(5))
(b) C Area ÷ Area Shaded is;
C area is;
2² - ½*4sin(90-2atan½) - ½*4sin(2atan½) - (180-2atan2)π/360 - ½*sin(2atan2)
= 4 - (6/5) - (8/5) - 0.463647609 - (2/5)
= 0.336352391 square units.
Area Shaded is;
2(½*1*2) - π(½(3-√(5)))² - (2atan2)π/360
= 2 - 0.458352191 - 1.10714871779
= 0.43449909121 square units.
Therefore;
C Area ÷ Area Shaded exactly in decimal is;
0.336352391 ÷ 0.4344990912
= 0.77411529232