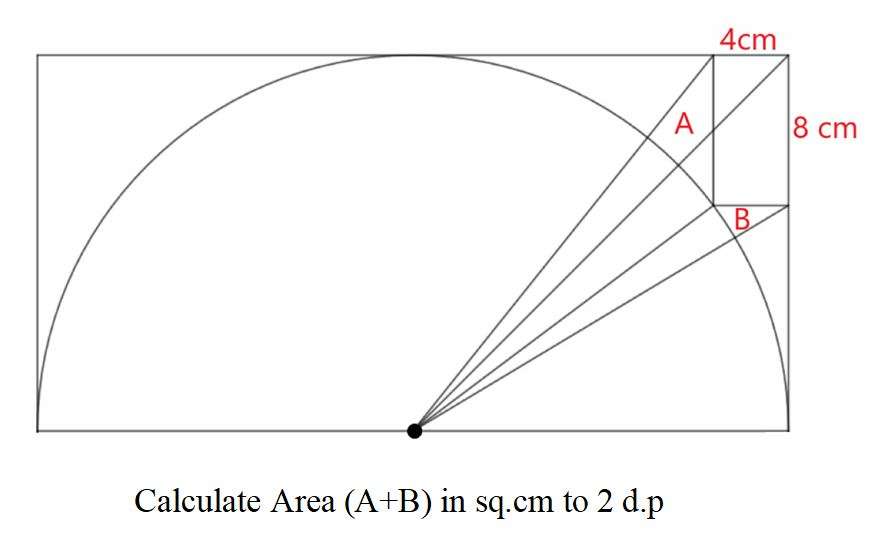
Mathematics Question and Solution
Let r be the radius of the inscribed semi circle.
Calculating r.
r² = (r-4)²+(r-8)²
r² = r²-8r+16+r²-16r+64
r²-24r+80 = 0
It implies;
r ≠ 4 cm.
r = 20 cm.
a² = 20²+16²
a = 4√(41) cm.
(4/sinb) = (4√(41)/sin45)
b = 6.34019174591°
c² = 2(20)²
c = 20√(2) cm.
Area A is;
½*4*20√(2)sin45 - ½(4²) - (6.34019174591*π*20²/360)
= 40 - 8 - 22.13144423478
= 9.86855576522 cm²
d = atan(20/12)
d = atan(5/3)°
Therefore;
e = atan(⅗)°
f² = 20²+12²
f = 4√(34) cm.
(4/sing) = (20/sin(atan⅗))
g = 5.90614111377°
Area B is;
0.5*4*4√(34)sin(atan⅗) - (5.90614111377π*400/360)
= 24 - 20.61632170454
= 3.38367829546 cm²
It implies;
Area (A+B) in cm² to 2 decimal places is;
9.86855576522 + 3.38367829546
= 13.25223406068
≈ 13.25 cm²