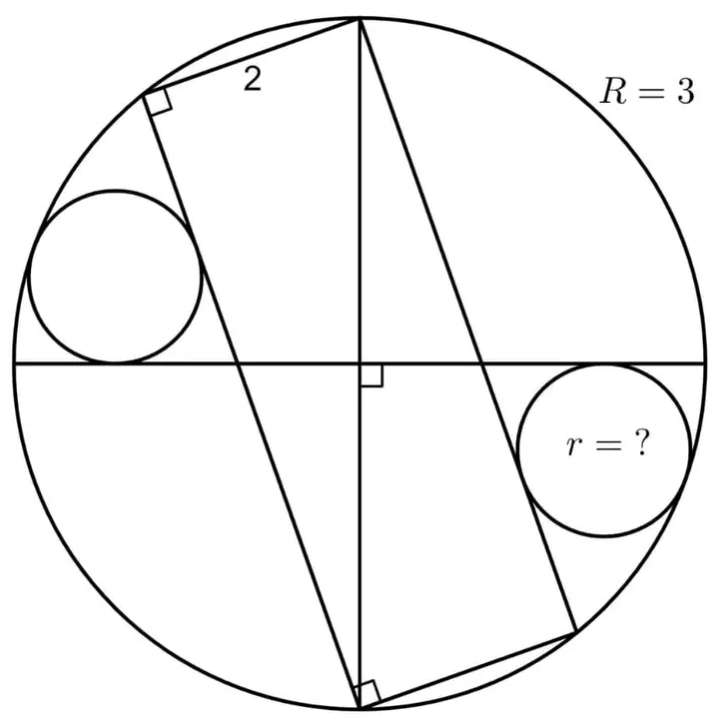
Mathematics Question and Solution
Diameter of the ascribed circle is;
2R
= 2*3
= 6 units.
a²+2² = 6²
a = √(32)
a = 4√(2) units.
Observing similar plane shape (right-angled) side length ratios.
3 - 4√(2)
b - 2
Cross Multiply.
4√(2)b = 6
b = 3/(2√(2))
b = ¾√(2) units.
b = 1.0606601718 units.
tanc = 3/1.0606601718
c = 70.5287793652°
d = ½(c)
d = 35.2643896826°
tan35.2643896826 = r/e
Where r is the required radius of the two congruent inscribed circles.
e = 1.4142135624r units.
e = √(2)r units.
f = (1.0606601718+1.4142135624r) units.
g = (3-r) units.
It implies;
Calculating r, radius of the two congruent inscribed circles is;
(3-r)² = r²+(1.0606601718+1.4142135624r)²
9-6r+r² = r²+1.125+3r+2r²
2r²+9r-7.875 = 0
2r²+9r-(73/8) = 0
16r²+72r-73 = 0
Resolving the above quadratic equation via completing the square approach to get r.
(r+(9/4))² = (73/16)+(81/16)
(r+(9/4))² = (154/16)
r+(9/4) = ±√(154/16)
r = -(9/4)±¼√(154)
It implies;
r = ¼(√(154)-9) units.
r = 0.8524184115 units.
Again, r is the radius of the two congruent inscribed circles.