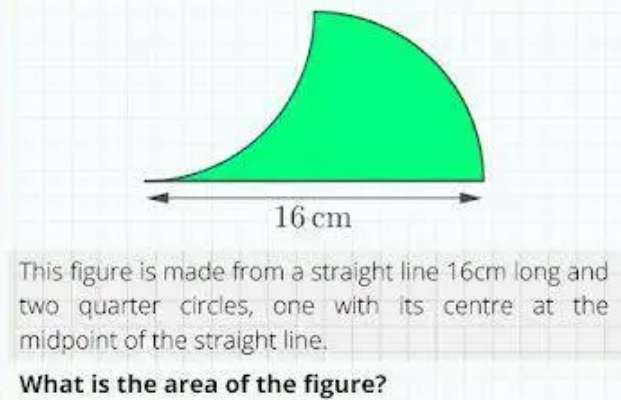
Notice.
The complete plane shape is half a circle with radius 8 cm.
Area green is;
Area semi circle with radius 8cm - 2(area quarter circle with radius 8 cm - area triangle with height and...
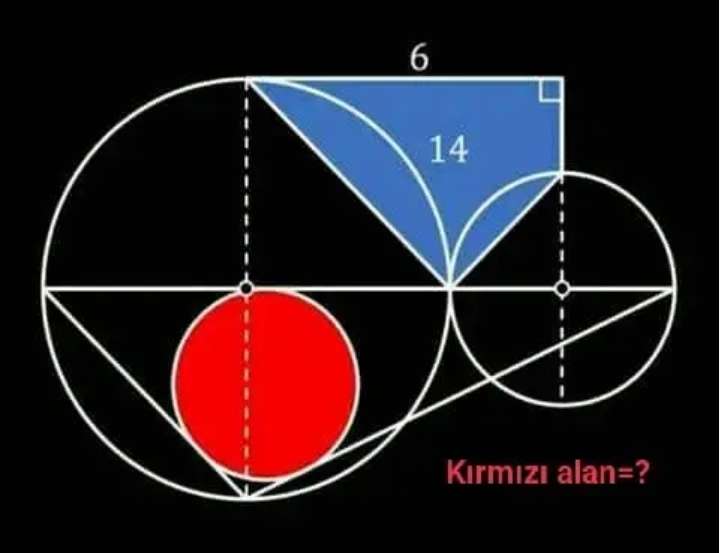
Calculating area of the inscribed red circle.
Let the bigger circle radius be a.
Let the big circle radius be b.
It implies;
a+b = 6 --- (1).
½(b²)+½(a²)+14 = 6*a
b²+a²+28 = 12a ---...
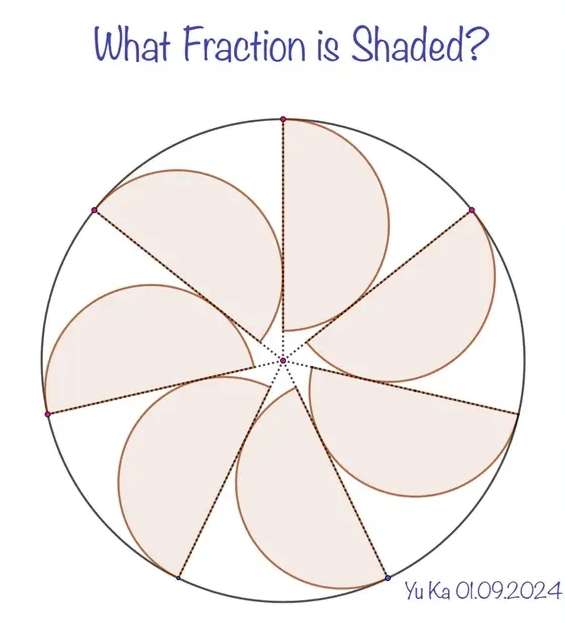
a = ⅐(360)°
a is the interior angle of each of the congruent 7 sectors.
Let the radius of the ascribed circle be 1 unit.
Area ascribed circle is;
π(1²)
= π square units.
c = (1-b) uni...
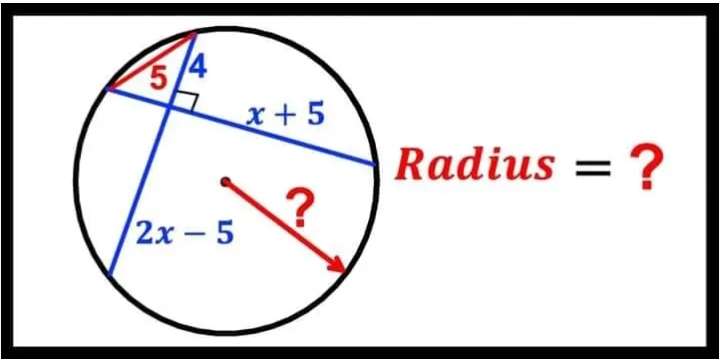
Calculating x.
a²+4² = 5²
a² = 25-16
a = 3 units.
Therefore;
3*(x+5) = 4*(2x-5)
3x+15 = 8x-20
5x = 35
x = 7 units.
It implies;
b = 3+x+5
And x = 7 units.
b = 3+7+5
b = 15 uni...
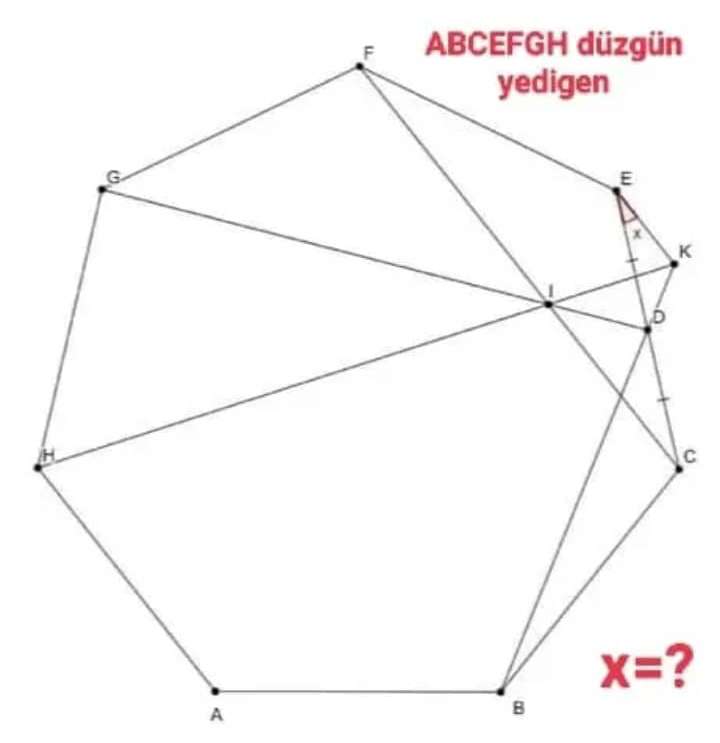
Calculating the required angle, x.
a = ⅐*180(7-2)
a = ⅐(900)
a is the single interior angle of the regular heptagon.
It implies, the required angle, x is;
Notice.
Length IC is paralle...
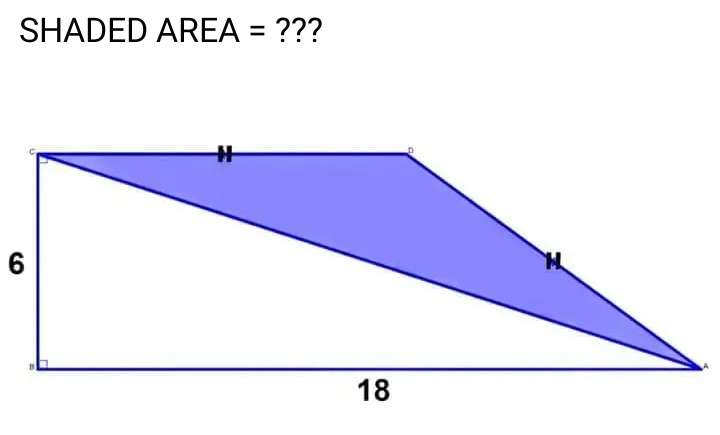
Calculating shaded area.
Let the equal lengths of the ascribed trapezoid be a.
Calculating a.
a² = 6²+(18-a)²
0 = 36+324-36a
36a = 360
a = 10 units.
Therefore, shaded area is;
½(1...
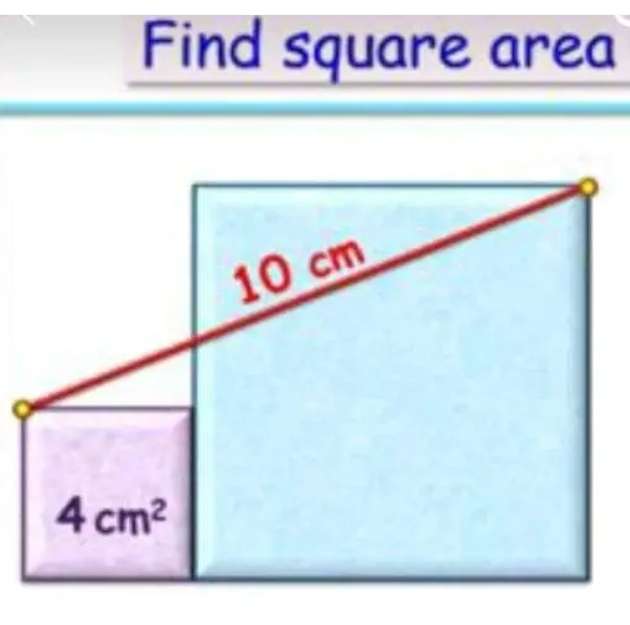
Calculating area of the bigger square.
Let the bigger square side length be a.
b² = 4
b = 2 cm.
b is the side length of the big square.
c = (a+2) cm.
d = (a-2) cm.
Calculating a²,...
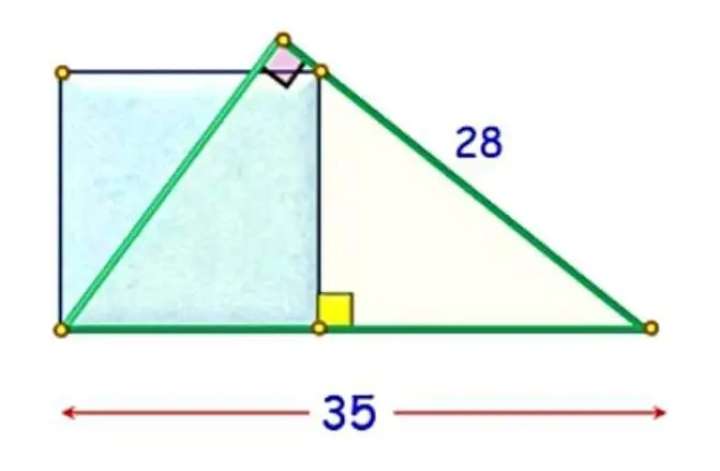
Calculating area of the square.
sina = 28/35
a = asin(28/35)°
b = a-45
b = (asin(28/35)-45)°
c²+28² = 35²
c² = 35²-28²
c = 21 units.
cos(asin(28/35)-45) = 21/d
d = 21.2132034356 un...
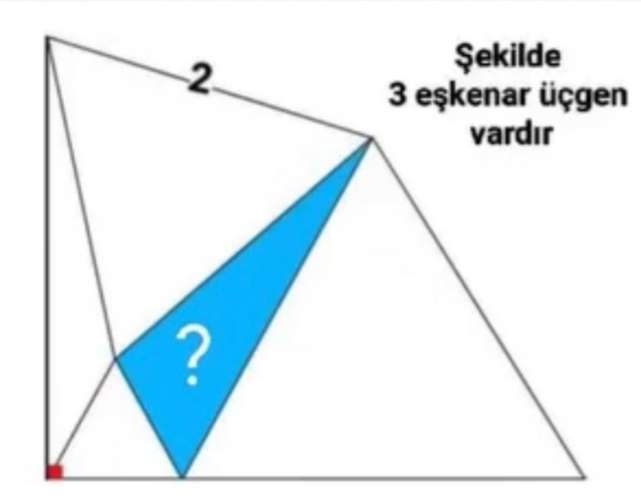
Let the side length of the big inscribed regular triangle be a.
It implies, the side length of the biggest inscribed regular triangle is 3a.
Calculating a.
2² = a²+(2a)²-2*a*2acos120
4 =...
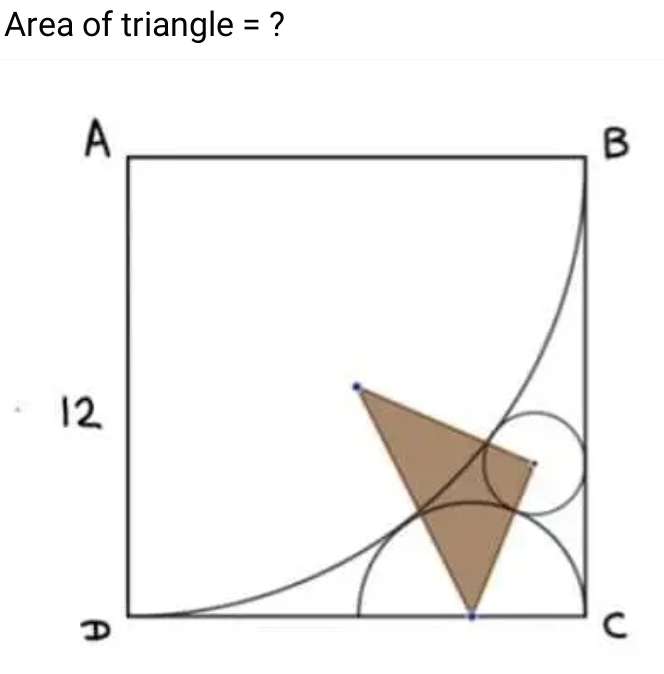
Let a be the radius of the inscribed half circle.
Let b be the radius of the inscribed circle.
c = (12+a) units.
d = (12-a) units.
Calculating a.
(12+a)² = 12²+(12-a)²
48a = 144
3a...