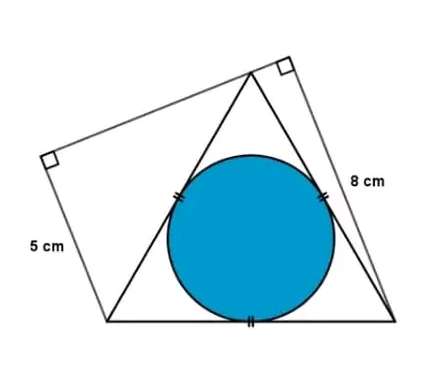
Mathematics Question and Solution
Calculating the area of the blue inscribed circle.
a = 8-5
a = 3 cm.
b²+3² = c²
c is the side length of the regular triangle.
b = √(c²-9) cm.
5²+d² = c²
d = √(c²-25) cm.
8²+e² = c²
e = √(c²-64) cm.
Notice!
d+e = b
√(c²-25)+√(c²-64) = √(c²-9)
It implies;
c = ⅓(14√(3)) cm.
c = 8.0829037687 cm.
Again, c is the side length of the inscribed regular triangle.
Calculating f, radius of the blue inscribed circle.
tan30 = f/(0.5*8.0829037687)
f = 2.3333333333 cm.
f = ⅓(7) cm.
Again, f is the radius of the blue inscribed circle.
Area blue inscribed circle is;
πf²
= π(⅓(7))²
= ⅑(49π) cm²