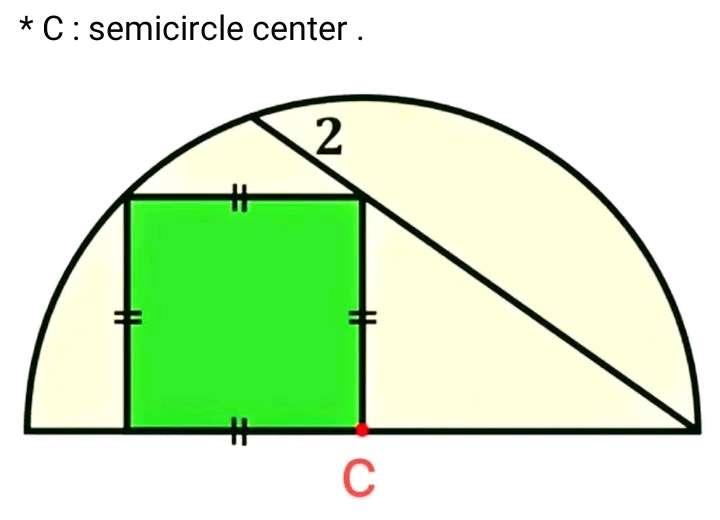
Mathematics Question and Solution
Let a be the side length of the inscribed square.
b² = 2a²
b = √(2)a units.
b is the radius of the half circle.
tanc = a/√(2)a
c = atan(1/√(2))°
d² = a²+(√(2)a)²
d² = a²+2a²
d = √(3)a units.
e = (2+√(3)a) units.
f = 2b
f = 2√(2)a
f = √(2)a unit.
Calculating a.
cos(atan(1/√(2))) = (2+√(3)a)/(2√(2)a)
0.8164965809 = (2+√(3)a)/(2√(2)a)
2.3094010767a-√(3)a = 2
0.5773502691a = 2
a = 3.4641016156 units.
a = 2√(3) units.
Again, a is the side length of the inscribed green square.
Area green square is;
a²
= (2√(3))²
= 12 square units.