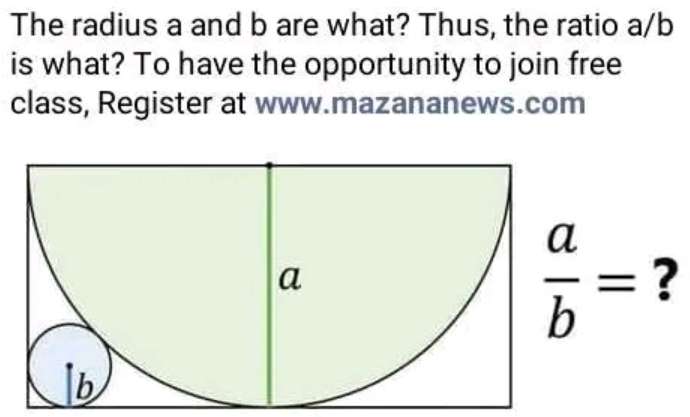
Let a be 2 unit.
b will be;
(2+b)²=2(2-b)²
4+4b+b²=8-8b+2b²
b²-12b+4=0
(b-6)²=-4+36
b = 6±√(32)
It implies;
b ≠ 6+√(32)
b = 6-√(32)
b = 6-4√(2)
b = 2(3-2√(2)) units.
Therefore;...

Let x be the radius of the inscribed green circle.
Therefore radius of the ascribed semi circle, r will be;
r = 2x
Therefore;
2*2=3x*x
4=3x²
x (green circle radius) is;
x = √(4...
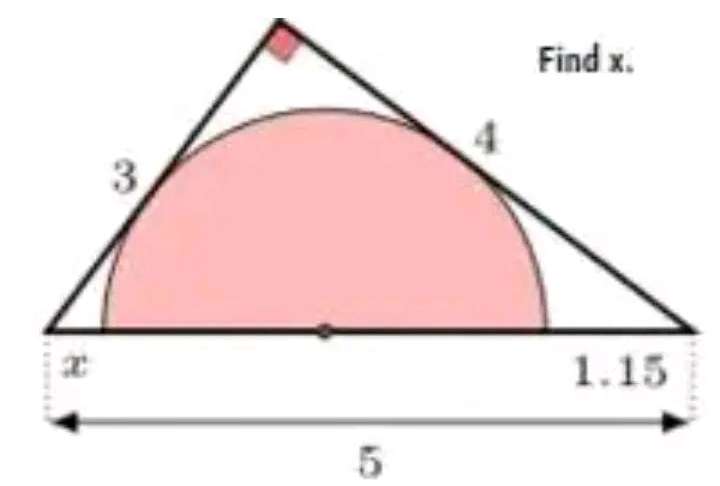
Calculating r, radius of the inscribed semi circle.
49r²-168r+144 = 0
Therefore;
r = 12/7 units.
It implies;
Calculating x.
x = 5-2(12/7)-(23/20)
x = 59/140 units.
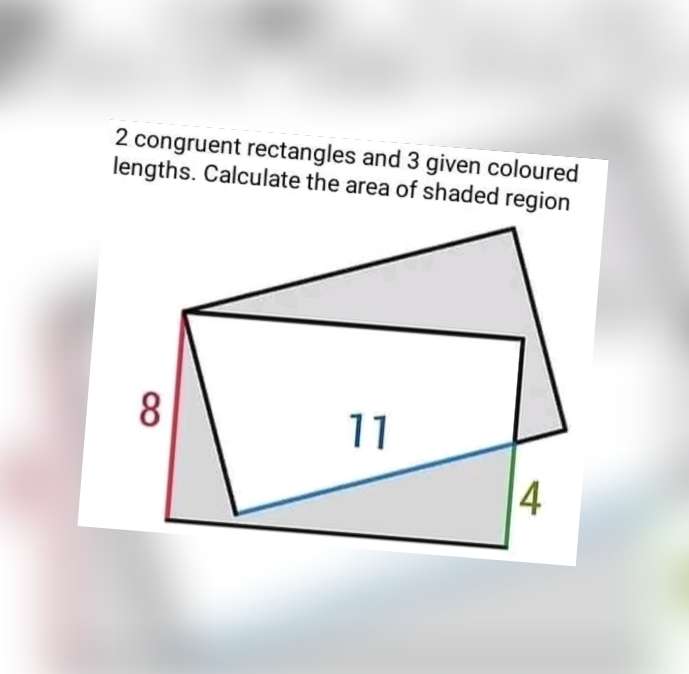
Shaded Area is;
(13*8)-½(11*8)-2(½(13*4))+½(2+13)*8
= 104-44-52+60
= 164-96
= 68 square units.
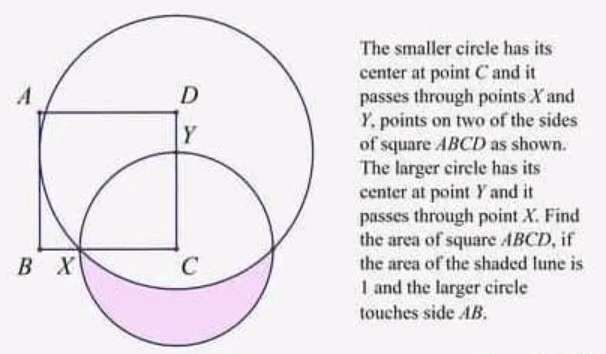
Let YC, radius of the small circle be r.
Notice;
XY = CD = AD = AB = BC = single side length of square ABCD.
Calculating r.
πr² - ½(πr²) - 90π(XY)²/360 + ½(XY)² = 1
XY will be;
√(r²+r²...
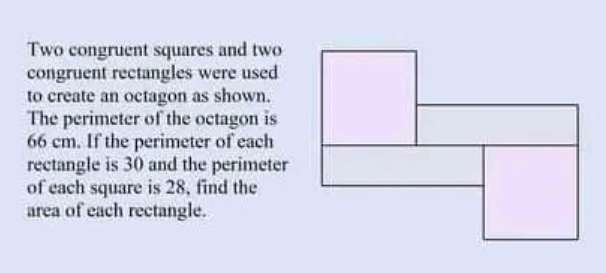
Let the length and width of the rectangle be y and z respectively.
Therefore;
7+7+x+y+z+7+7+x+y+z=66
Where 7 is the single side length of the square.
It implies;
14+14+2x+2y+2z=66
Th...
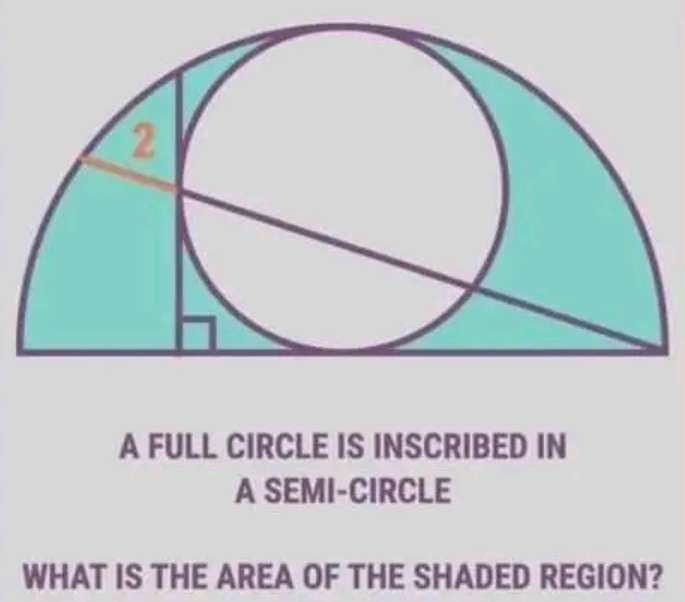
Let the radius of the semi circle be r.
Calculating r.
2+√(5/2)r - ½(3r)
2r - √(5/2)r
Cross multiply.
3r² = 2√(5/2)r + (5/2)r²
(½)r² = 2√(5/2)r
(¼)r² = √(5/2)r
(1/16)r⁴...
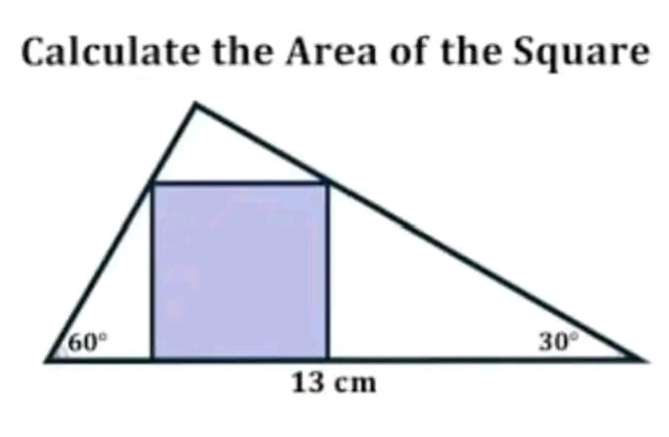
Let a be the side length of the inscribed square.
Calculating a², area of the inscribed square.
tan60 = a/b
b = ⅓(√(3)a) cm.
tan30 = a/c
c = √(3)a cm.
Calculating a.
It implies;...
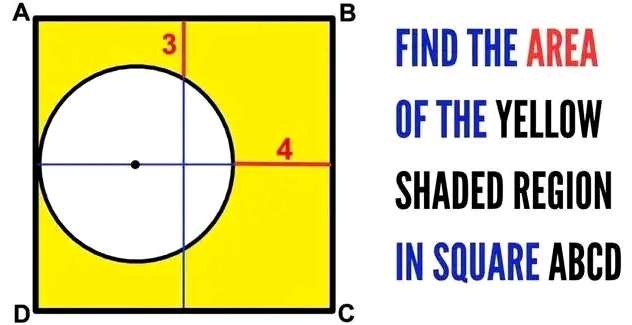
Let a be the radius of the inscribed circle.
b = (2a+4) units.
b is the side length of the square.
c = ½(b)
c = (a+2) units.
d = c-a
d = 2 units.
e = c-3
e = (a+2)-3
e = (a-1) unit...
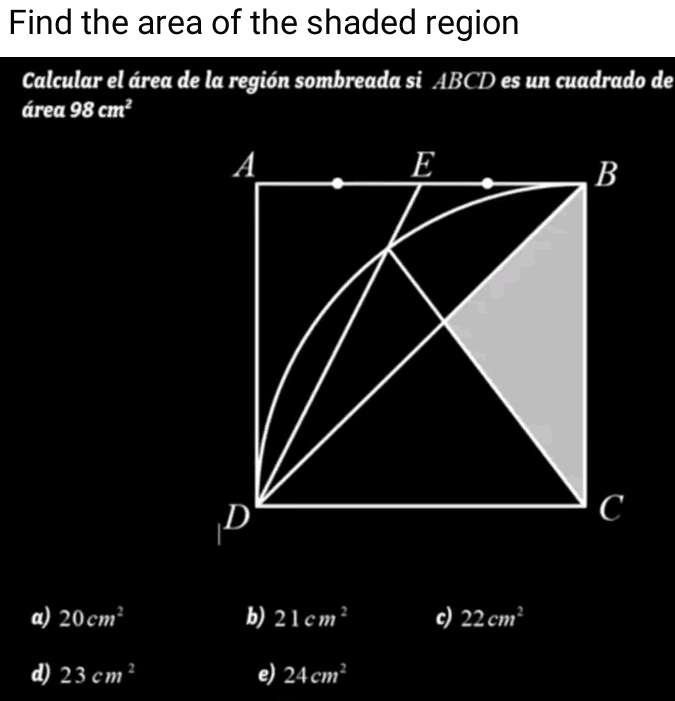
Let a be the side length of the square.
a² = 98
a = √(98)
a = 7√(2) cm.
tanb = (0.5*7√(2))/(7√(2))
b = atan(1/2)°
c = 90-b
c = atan(2)°
d = 45-b
d = (45-atan(1/2))°
e = 180-(45-...