
Sir Mike Ambrose is the author of the question.Calculating Area Red : Area Green : Area Blue.Let AB be 2 units.Therefore CD = 1 unit.It implies;Area Blue is;Area triangle with height 0.72111025509 un...

Sir Mike Ambrose is the author of the question.Calculating Area brown exactly in square unit decimal is;Area brown exactly in square unit decimal is;Area triangle with height 2 unit and base (1.93220...
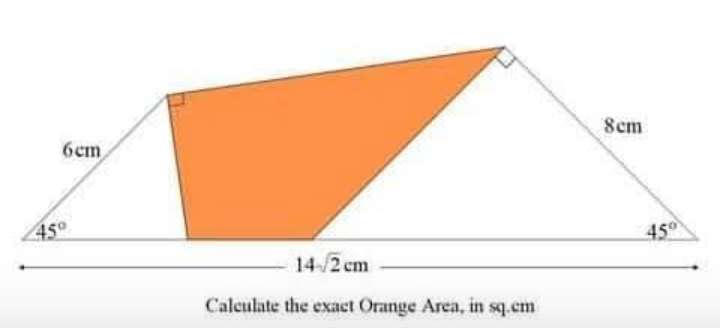
Sir Mike Ambrose is the author of the question.Area orange exactly in cm² decimal form is;Area triangle with height 10 cm and base 4.28571428571 cm + Area triangle with height 8 cm and base (3.636549...
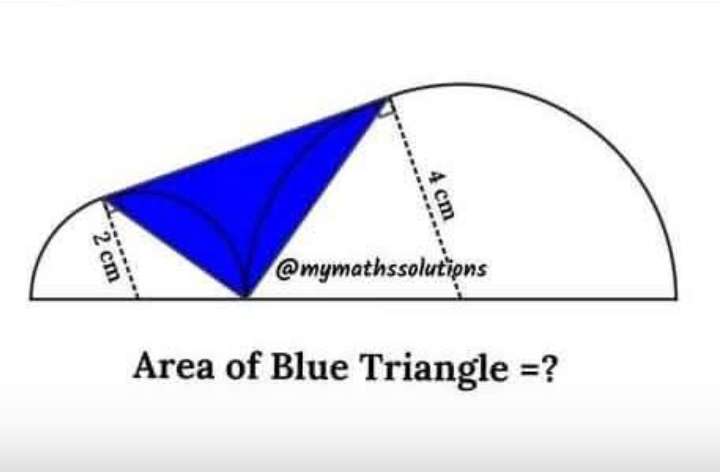
Calculating x, the length that form tangents of the two semi circles.x²+2²=6²x²=36-4x²=32x = √(32) cm.x = 4√(2) cm.Therefore;Area blue is;Area trapezium with two parallel length 2 cm and 4 cm, and he...
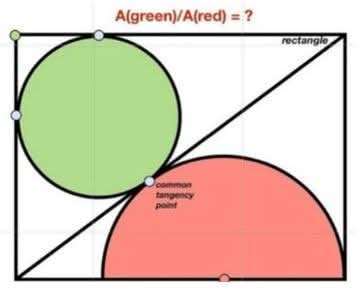
Calculating Area Green ÷ Area Red.Let 2 units be the length of the ascribed rectangle.Let x be the radius of the green inscribed circle.Let y be the radius of the red inscribed half circle.Notice.a =...
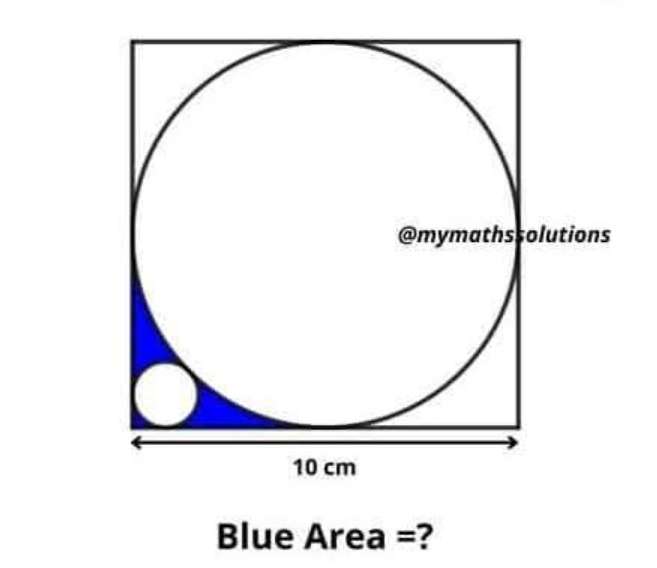
Calculating radius, r of the small inscribed circle.2r² = (5√(2)-5-r)²r = (5√(2)-5)*(√(2)-1)r = (15-10√(2)) cmTherefore blue area is;Area square with side 5 cm - Area quarter circle with radius 5 cm...
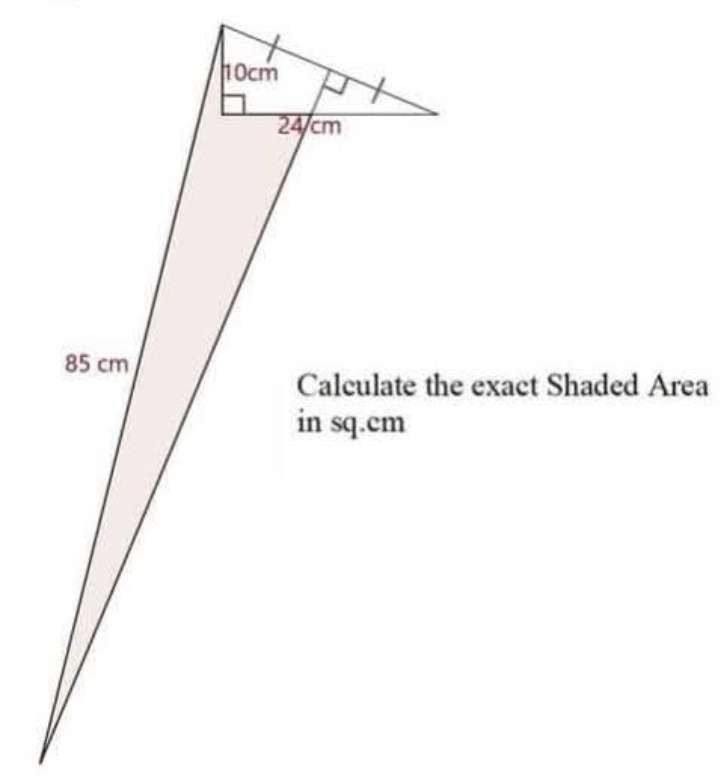
Sir Mike Ambrose is the author of the question.Calculating Shaded Area.Shaded area exactly in cm² is;Area triangle with height 84 cm and base 13 cm - Area triangle with height 10 cm and base 24 cm +...
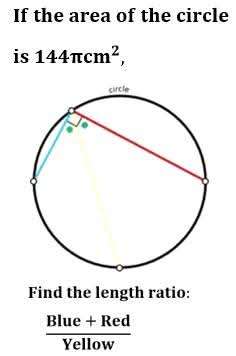
Calculating (length Blue + length red)/(length yellow).Let r be the radius of the circle.Calculating r.πr² = 144πr² = 144r = 12 cm.a = 2ra = 24 cm.a is the diameter of the circle.Let b be the blue le...
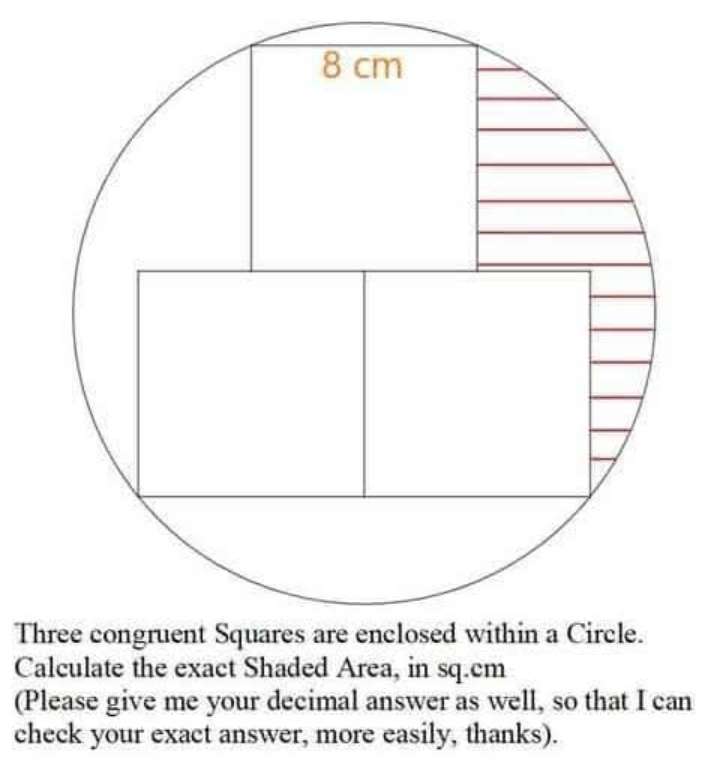
Sir Mike Ambrose is the author of the question.Calculating r, radius of the circle.Radius of the circle, r is;r² = (8+(3/2))²+4²r² = (19/2)²+16r² = ¼(425)r = ½(5√(17)) cmTherefore;Area shaded, exactl...
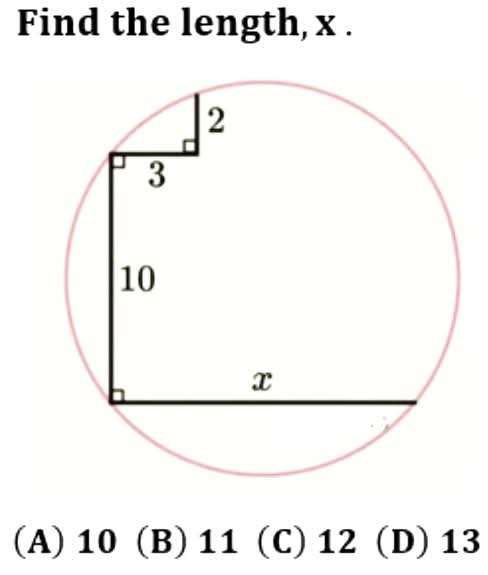
Calculating length x.12*2 = 3(x-3)24 = 3(x-3)24 = 3x-933 = 3xx = 11 units.