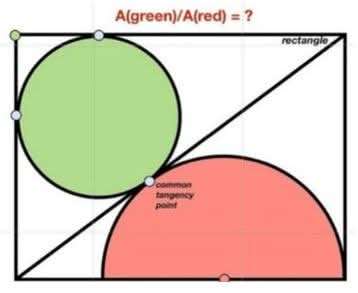
Mathematics Question and Solution
Calculating Area Green ÷ Area Red.
Let 2 units be the length of the ascribed rectangle.
Let x be the radius of the green inscribed circle.
Let y be the radius of the red inscribed half circle.
Notice.
a = 2y units.
a is the width of the ascribed rectangle.
b = (2-y) units.
c²+y² = (2-y)²
c² = 4-4y+y²-y²
c = √(4-4y) units.
d = x+c
d = (x+√(4-4y)) units.
Notice.
d = a
It implies;
(x+√(4-4y)) = 2y
x = (2y-√(4-4y)) units.
x is the radius of the green circle.
e² = 2²+(2y)²
e = √(4+4y²) units.
e is the diagonal of the ascribed rectangle.
f = c+2y
f = (√(4-4y)+2y) units.
Calculating y.
It implies;
e = f, the diagonal of the ascribed rectangle.
Therefore;
√(4+4y²) = √(4-4y)+2y
4+4y² = (√(4-4y)+2y)²
4+4y² = 4-4y+4y√(4-4y)+4y²
4 = 4-4y+4y√(4-4y)
0 = -4y+4y√(4-4y)
4y = 4y√(4-4y)
1 = 4-4y
4y = 3
y = ¾ units.
Again, y is the radius of the red half circle.
Calculating x, radius of the green circle.
Recall.
x = (2y-√(4-4y)) units.
And y = ¾ units.
x = 2(¾)-√(4-4(¾))
x = (3/2)-√(1)
x = (3/2)-1
x = ½ units.
Again, x is the radius of the green circle.
Therefore, Area Green ÷ Area Red is;
πx²÷(½*πy²)
(π(½)²)÷(½*π(¾)²)
= (¼)*(32/9)
= 8/9