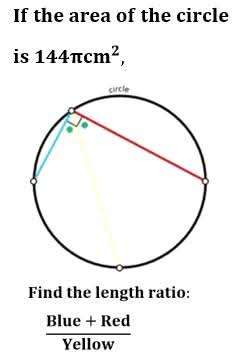
Mathematics Question and Solution
Calculating (length Blue + length red)/(length yellow).
Let r be the radius of the circle.
Calculating r.
πr² = 144π
r² = 144
r = 12 cm.
a = 2r
a = 24 cm.
a is the diameter of the circle.
Let b be the blue length.
A sincere study of the plane shape derives a regular hexagon inscribing the circle with blue side length b each length.
Notice.
The single six interior angles of the regular hexagon is 120° each.
Let c be the red length.
c²+b² = 24²
c = √(576-b²) units.
Calculating b.
√(576-b²)² = b²+b²-2*b*bcos120
576-b² = 2b²+b²
4b² = 576
b² = 144
b = 12 units.
Again, b is the blue length.
Recall.
c = √(576-b²) units.
And b = 12 units.
c = √(576-12²)
c = √(576-144)
c = √(432)
c = 12√(3) units.
c = 20.7846096908 units.
Again, c is the red length.
Calculating d, the yellow length.
e²+e² = 24²
2e² = 576
e² = 288
e = 12√(2) units
Length yellow is;
(12√(2))² = 12²+d²-2*12*dcos45
288 = 144+d²-12√(2)d
d²-12√(2)d-144 = 0
(d-6√(2))² = 144+(-6√(2))²
(d-6√(2))² = 144+72
(d-6√(2))² = 216
d-6√(2) = ±√(216)
d = 6√(2)±6√(6)
It implies;
d ≠ 6√(2)-6√(6)
d = 6√(2)+6√(6)
d = 6√(2)(1+√(3)) units.
d = 23.1822198309 units.
Again, d is yellow length.
Therefore, (length Blue + length red)/(length yellow) is;
(12+12√(3))/(6√(2)(1+√(3)))
= 12(1+√(3))/(6√(2)(1+√(3)))
= 12/(6√(2))
= 2/√(2)
= √(2)