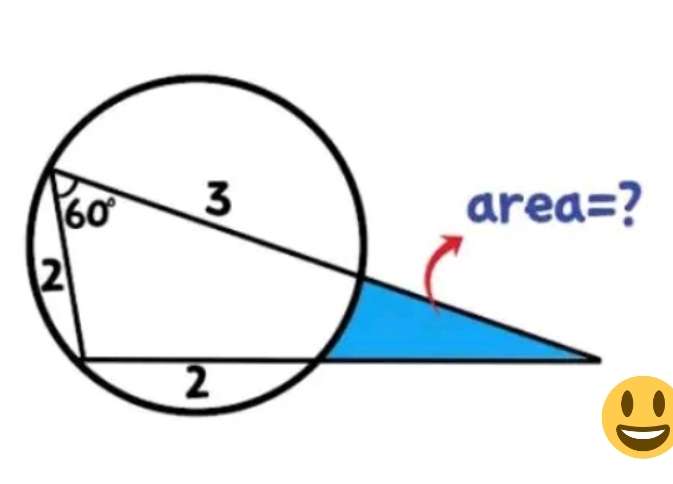
a = 180-60
a = 120°
b² = 2²+3²-2*2*3cos60
b² = 13-6
b = √(7) units.
(√(7)/sin120) = (2/sinc)
c = 40.8933946491°
d = 60-c
d = 19.1066053509°
(√(7)/sin60) = (2/sine)
e = 40.893394649...
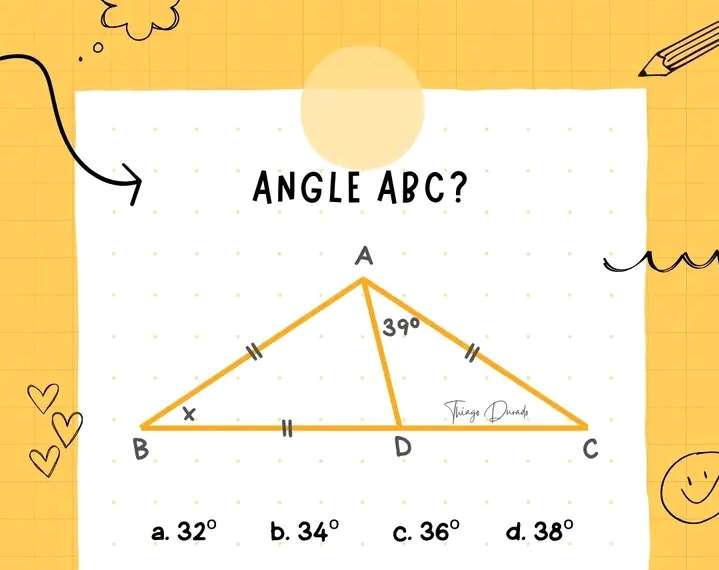
Calculating x, angle ABD
a = ½(180-x)°
a is angle BAD.
It implies;
x, angle ABD is,
x+x+(a+39) = 180 (sum of the interior angles of the ascribed triangle)
2x+½(180-x) = 180-39
2x+½(180-x)...
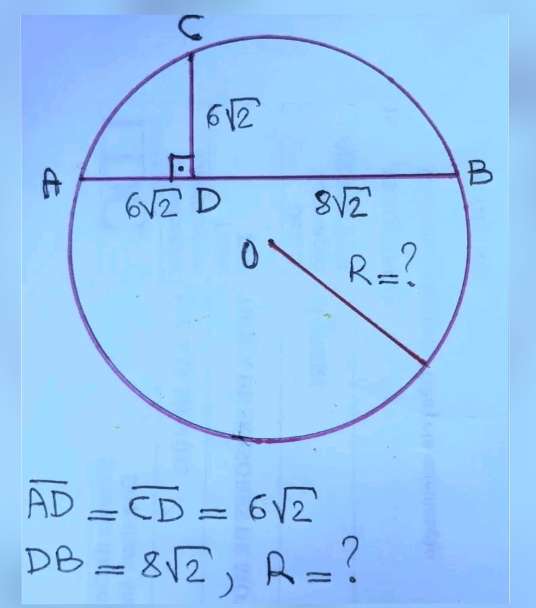
Calculating R, radius adius of the circle.
b = ½(6√(2)+8√(2))
b = 7√(2) units.
c = b-6√(2)
c = √(2) units.
It implies;
R² = c²+b²
R² = √(2)²+(7√(2))²
R² = 2+98
R = √(100)
R = 10 units.
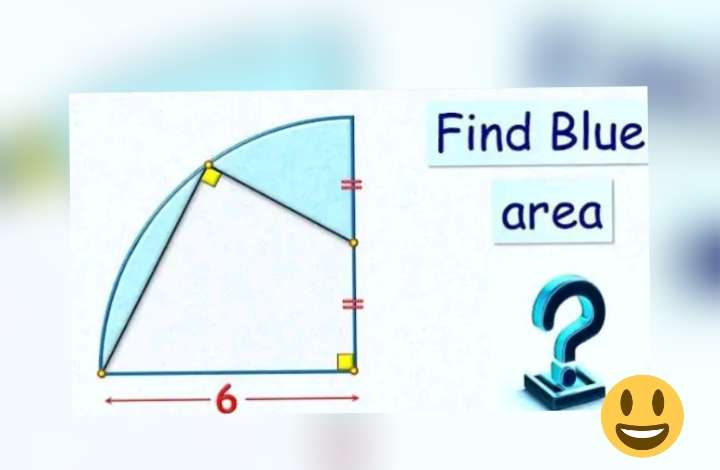
a² = 6²+(0.5*6)²
a² = 36+9
a = √(45)
a = 3√(5) units.
Observing similar plane shape (right-angled) side length ratios.
3√(5) - (6+6)
3 - b
Cross Multiply.
3√(5)b = 12*3
b = ⅕(12√(5)) u...
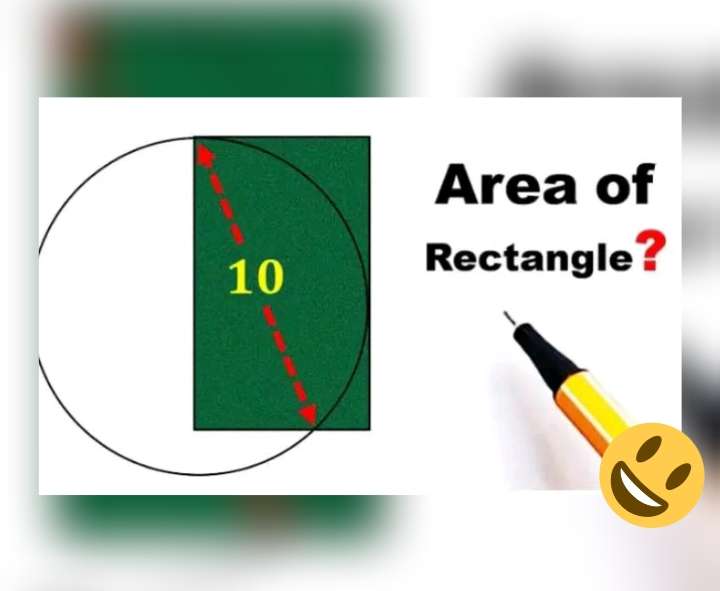
Let a be the radius of the circle and also, the width of the green rectangle.
b = 180-45
b = 135°
c = ½(45)
c = 22.5°
It implies;
cos22.5 = d/10
d = 9.2387953251 units.
d is the len...
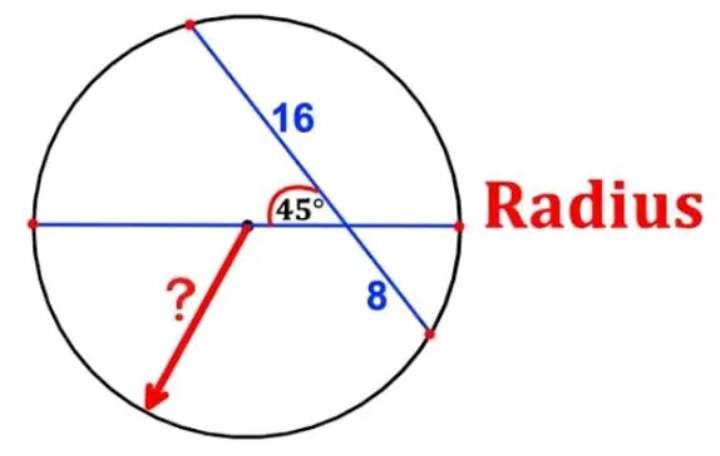
Let a be the radius of the circle.
It implies;
a² = 16²+b²-2*16bcos45
a² = 256+b²-16√(2)b --- (1).
a² = 8²+b²-2*8bcos135
a² = 64+b²+8√(2)b --- (2).
Equating (1) and (2) to get b.
2...
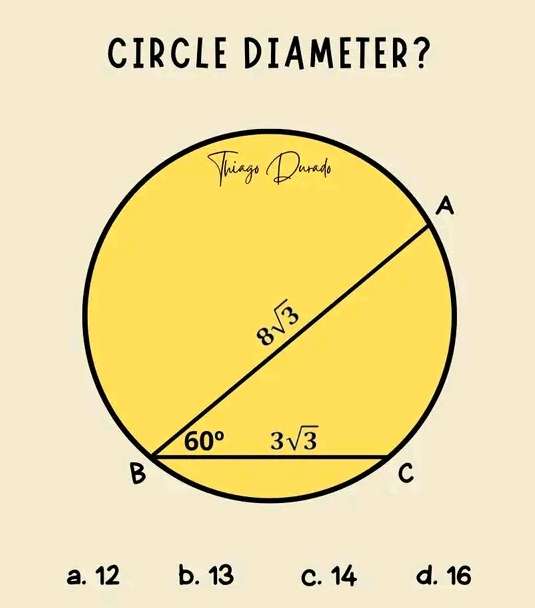
a² = (8√(3))²+(3√(3))²-2*8√(3)*3√(3)cos60
a = 7√(3) units.
a = 12.124355653 units.
a is AC.
(7√(3)/sin60) = (8√(3)/sinb)
b = 81.7867892983°
c = 180-b
c = 98.2132107017°
c is angle ACB....
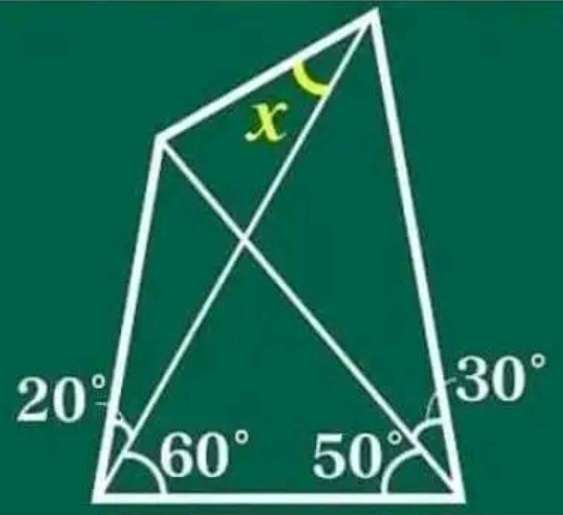
x = 30°
Please, move the above question left/right one time to review the solution.
Thank you.
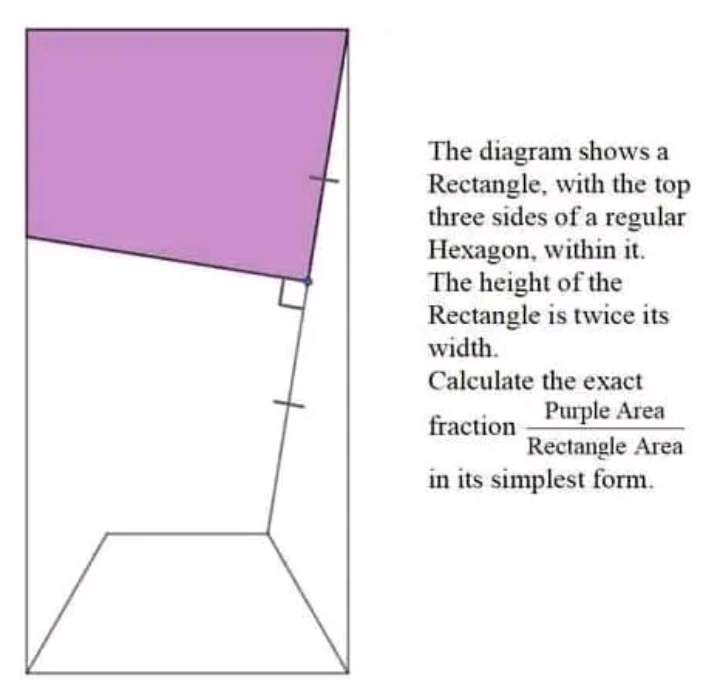
Let the single side length of the three side regular hexagon be 1 unit.
Therefore;
The width of the rectangle is;
2 units.
The length/height of the rectangle is;
4 units.
It impli...
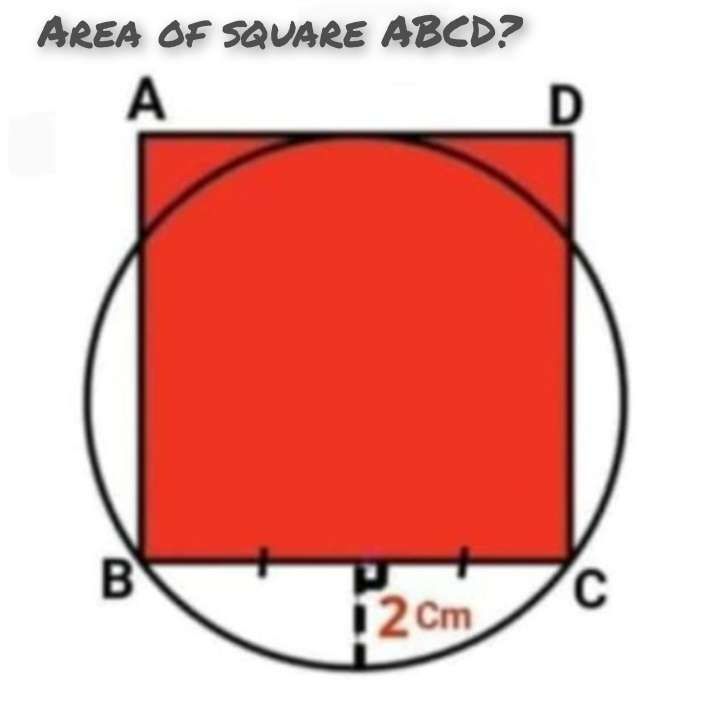
Let the radius of the circle be a.
b = (a-1) cm.
c = (a-2) cm.
It implies, observing Pythagoras rule to get a, radius of the circle.
a² = b²+c²
a² = (a-1)²+(a-2)²
a² = a²-2a+1+a²-4a+4...