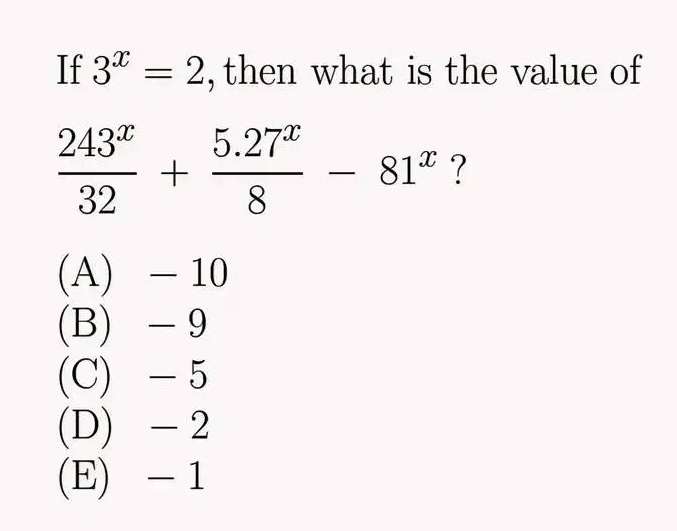
Prime multiples of 243 is;
3*3*3*3*3*3 = 3⁵ in index form.
Prime multiples of 27 is;
3*3*3 = 3³ in index form.
Prime multiples of 81 is;
3*3*3*3 = 3⁴ in index form.
And 3^(x) = 2
Ther...
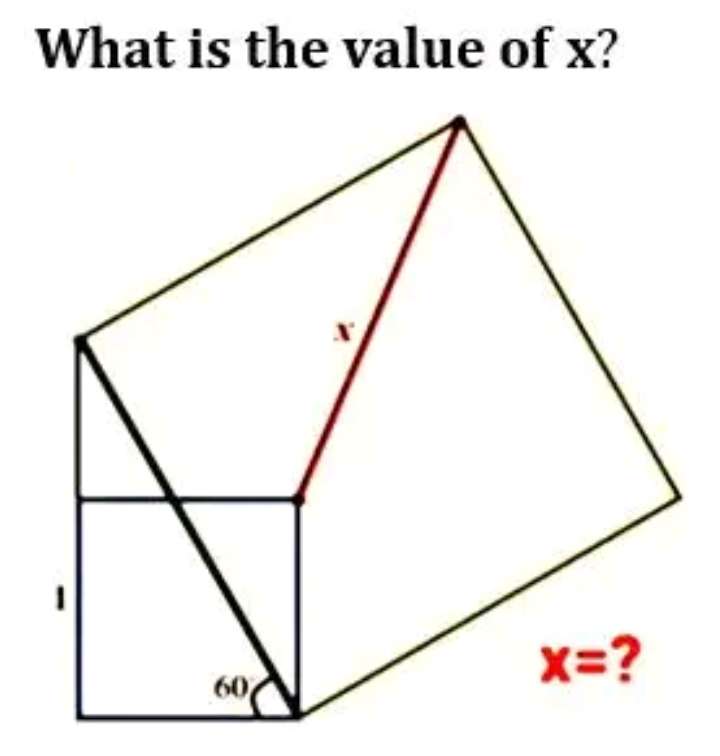
Notice!
The composite plane shape consist of two squares.
Calculating length x.
Sin30 = 1/a
a = 2 units.
a is the side length of the bigger square.
b² = 2a²
b² = 2(2²)
b = √(8)
b = 2√(2)...
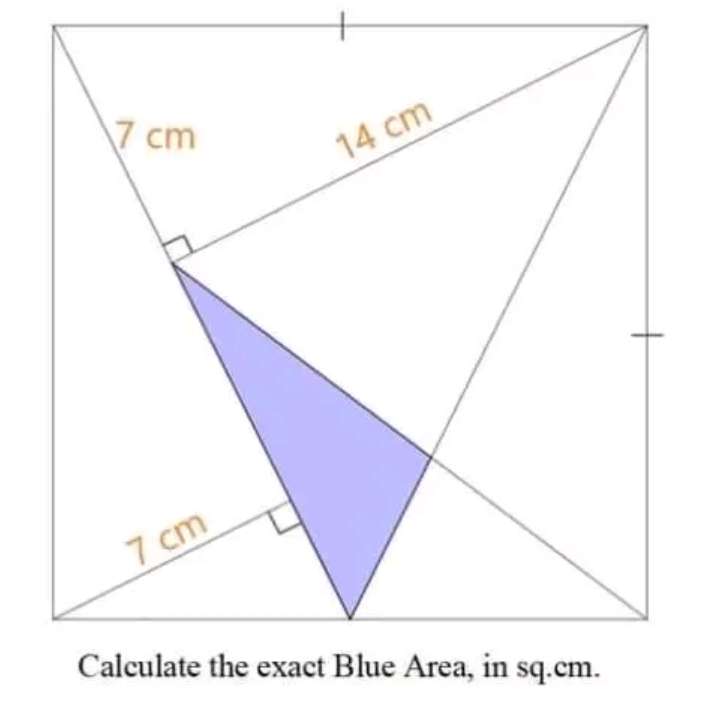
Sir Mike Ambrose is the author of the question.
Area Blue is;
Area triangle with two side length 10½ unit and ((7√(5)sin(atan(3/4)))/(2sin(180-atan(2)-atan(3/4))) unit, and angle (180-2atan(2...
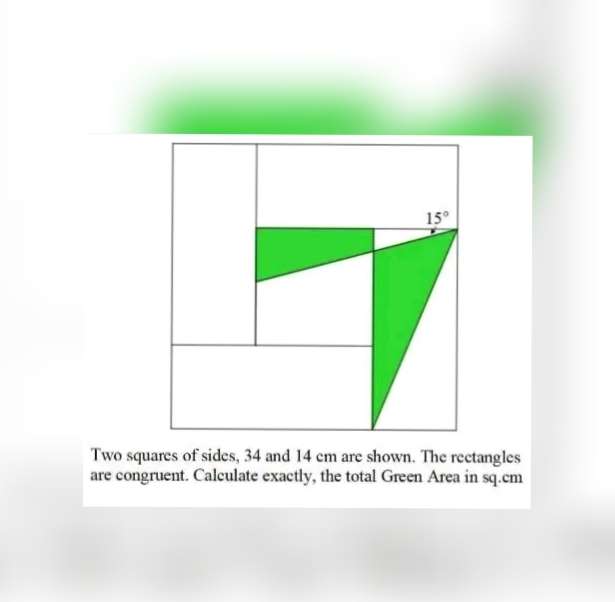
Sir Mike Ambrose is the author of the question.
Area Green total, exactly in cm² is;
Area triangle with height 24 cm and base 10 cm + Area triangle with height 24 cm and base (24tan15) cm - 2...
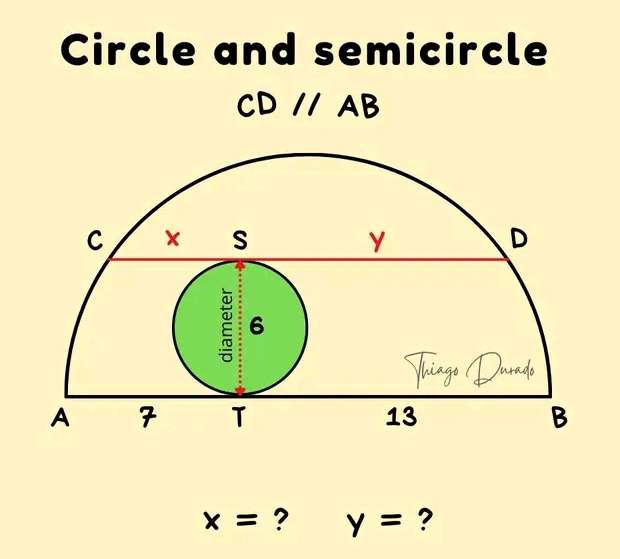
a = ½(7+13)
a = 10 units.
a is the radius of the ascribed semi circle.
b = 10-7
b = 3 units.
Calculating y.
10² = c²+6²
c² = 64
c = 8 units.
y = b+c
y = 11 units.
Calculating x...
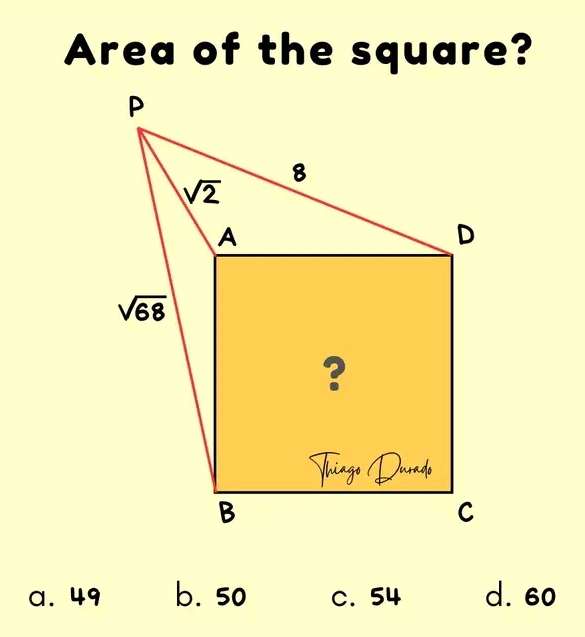
Let the square side length be a.
It implies;
Area square is a²
Calculating a² (Area of the Square).
√(2)² = b²+c²
c = √(2-b²) --- (1).
√(68)² = (a+b)²+c²
68 = (a+b)²+√(2-b²)²
68 = (...

a = 180-60
a = 120°
(7/sin120) = (3/sinb)
b = 21.7867892983°
c = 60+b
c = 81.7867892983°
d = 180-120-b
d = 60-21.7867892983
d = 38.2132107017°
(7/sin120) = (e/sin38.2132107017)
e...

Sir Mike Ambrose is the author of the question.
Area rectangle is;
9x8 = 72 square unit.
Area green is;
Area trapeziod with two parallel lengths (5+2-¾) unit and height 5 unit - Area sect...

Blue Area will be;
2(area circle of radius 1 unit - 2(2(area sector of radius 1 unit and angle 60°) - area equilateral triangle of two side length 1 unit and angle 60°))
= 2(π - 2(2(π/6) - ¼...
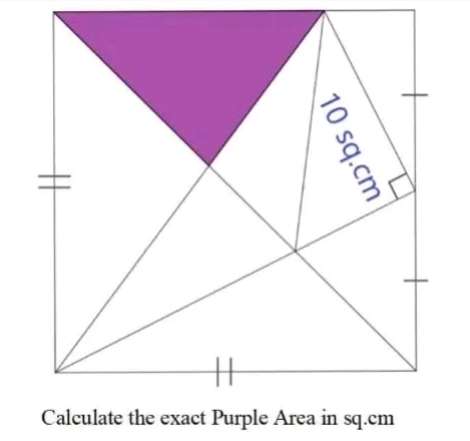
Sir Mike Ambrose is the author of the question.
Let the side length of the square be a.
tanb = a/(0.5a)
b = atan(2)°
c = 180-b-45
c = (135-atan(2))°
(0.5a/sin(135-atan(2)) = (d/sin45)...