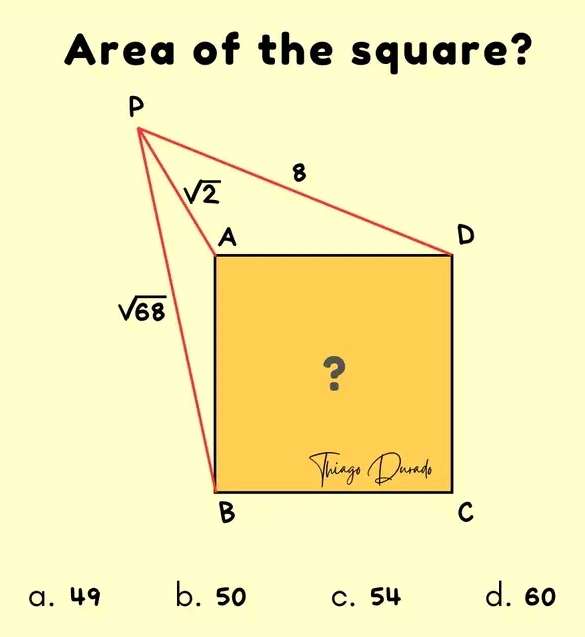
Mathematics Question and Solution
Let the square side length be a.
It implies;
Area square is a²
Calculating a² (Area of the Square).
√(2)² = b²+c²
c = √(2-b²) --- (1).
√(68)² = (a+b)²+c²
68 = (a+b)²+√(2-b²)²
68 = (a+b)²+2-b²
66 = a²+2ab --- (2).
8² = b²+(c+a)² --- (3).
64 = b²+c²+2ac+a²
64 = b²+(√(2-b²)²+2a√(2-b²)+a²
64 = b²+2-b²+2a√(2-b²)+a²
62 = 2a√(2-b²)+a²
(62-a²)² = 4a²(2-b²)
3844-124a²+a⁴ = 8a²-4a²b²
132a²-3844-a⁴= 4a²b²
b² = (132a²-3844-a⁴)/(4a²)
b = √(132a²-3844-a⁴)/2a --- (3).
Substituting (3) in (2).
66 = a²+2ab
And b = √(132a²-3844-a⁴)/2a
Therefore;
66 = a²+2a√(132a²-3844-a⁴)/2a
66 = a²+√(132a²-3844-a⁴)
(66-a²)² = 132a²-3844-a⁴
4356-132a²+a⁴ = 132a²-3844-a⁴
2a⁴-264a²+8200 = 0
a⁴-132a²+4100 = 0
Let a² be p.
It implies;
p²-132p+4100 = 0
Calculating p via completing the square approach.
(p-66)² = -4100+(-66)²
(p-66)² = 256
p = 66±√(256)
p = 66-16 = 50 units.
Or
p = 66+16 = 82 units.
And p = a²
It implies;
a² ≠ p ≠ 82
a² = p = 50 square units.
a² = 50 square units
Again, a² is the area of the square.