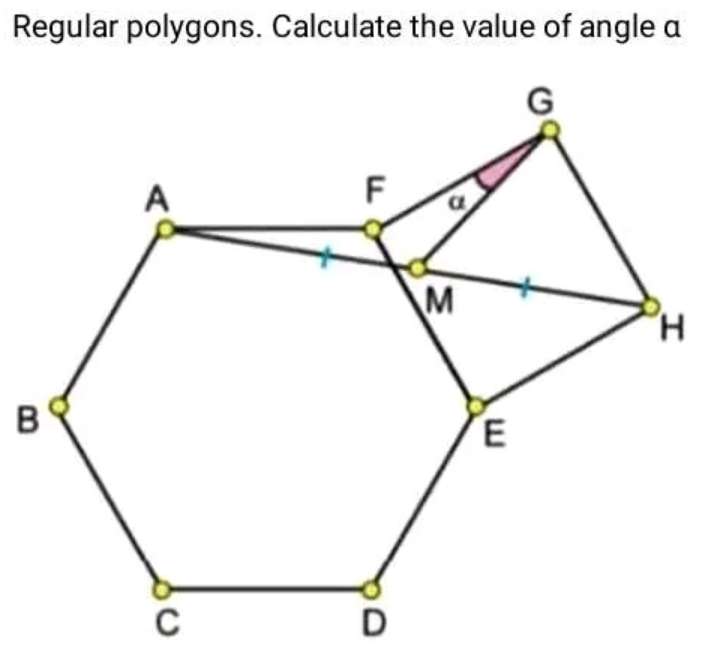
Let the single side length of the hexagon be 2 units.
Therefore;
AG =√(8-8cos150) units.
Calculating AH.
AH = √((8-8cos150)+4-4√(8-8cos150)cos105)
AH = 4.78834034195 units
Therefor...
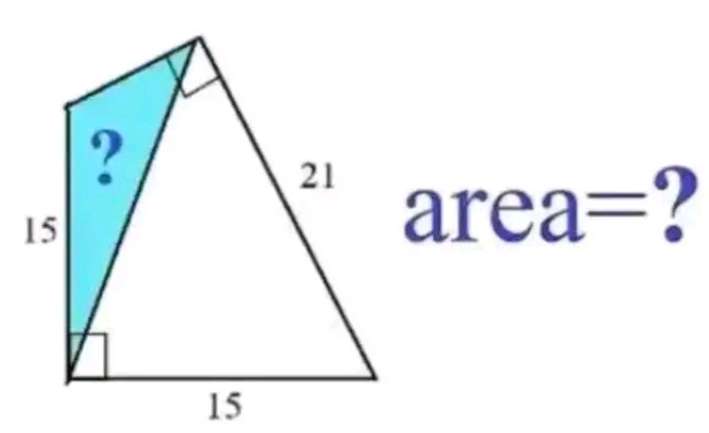
a² = 2(15)²
a = √(2(15)²)
a = 15√(2) units.
b²+21² = a²
b² = 450-441
b² = 9
b = 3 units.
tanc = 15/15
c = 45°
tand = 3/21
d = atan(1/7)°
e = 180-c-d
e = 135-atan(1/7)
e = (45+a...
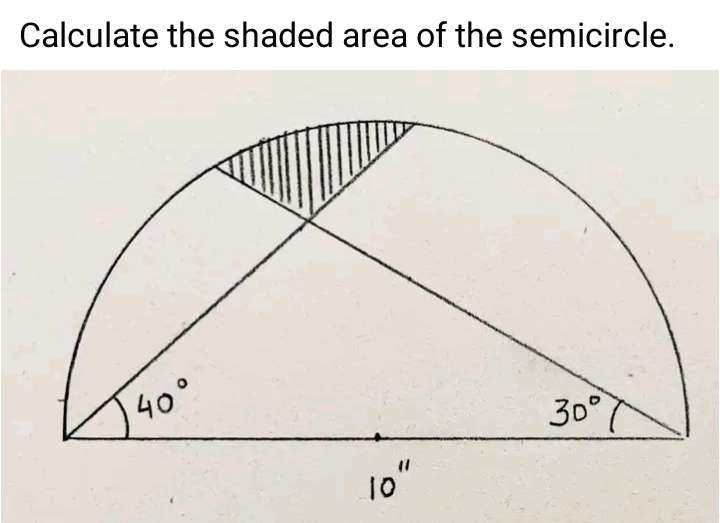
cos30 = a/10
a = 5√(3) units.
sin30 = b/10
b = 5 units.
cos40 = c/10
c = 7.6604444312 units.
sin40 = d/10
d = 6.4278760969 units.
e = 180-30-40
e = 110°
(10/sin110) = (f/sin30)...
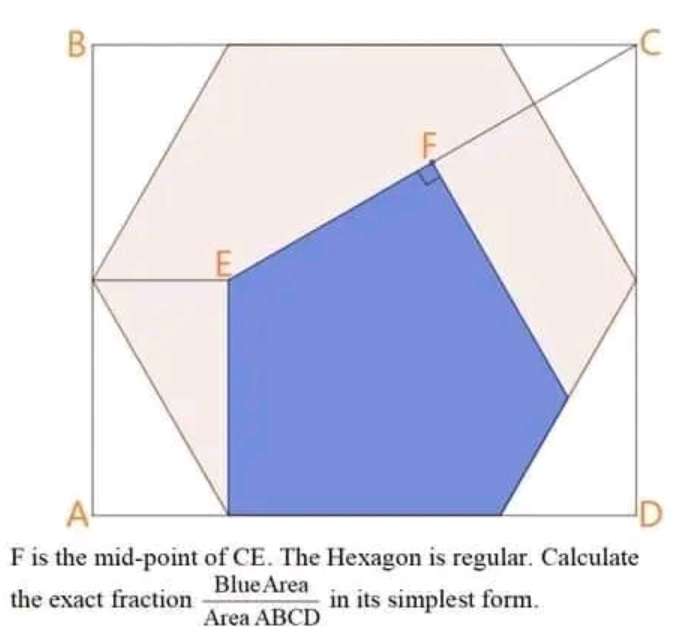
Sir Mike Ambrose is the author of the question.
Let the single side length of the inscribed regular hexagon be 2 units.
Therefore;
Area rectangle ABCD is:
2√(3) * 4
= 8√(3) square units....
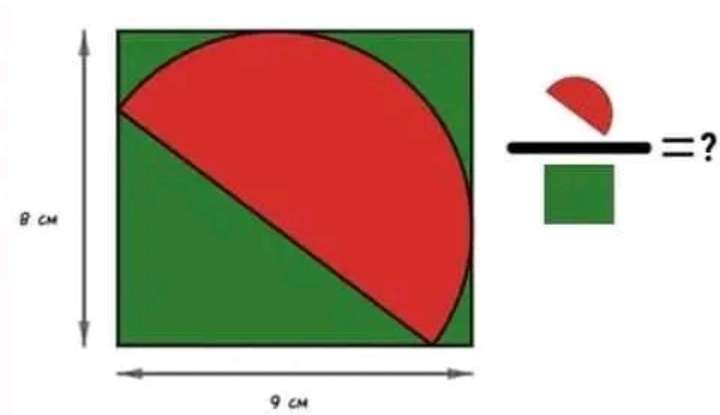
Let the radius of the inscribed red semi circle be r.
Therefore;
(8-r)²+(9-r)²=r²
64-16r+r²+81-18r+r²=r²
r²-34r+145=0
(r-17)²=-145+(17)²
r = 17±√(144)
r = 17±12
It implies ;
r ≠ 29 cm....
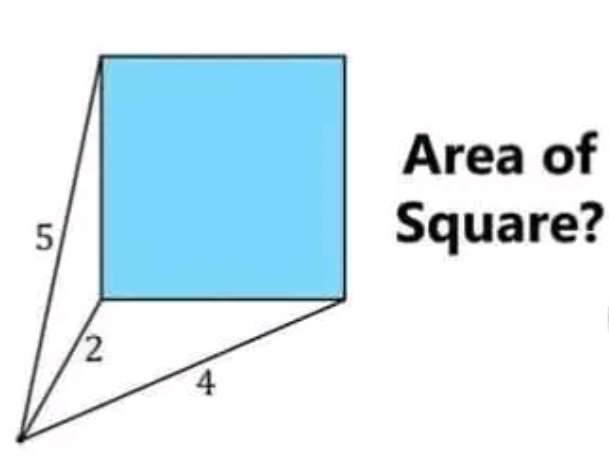
Blue Area/Square is;
½(41-√(511)) square unit.
Please, move the above question left/right twice to review the solution.
Thank you.
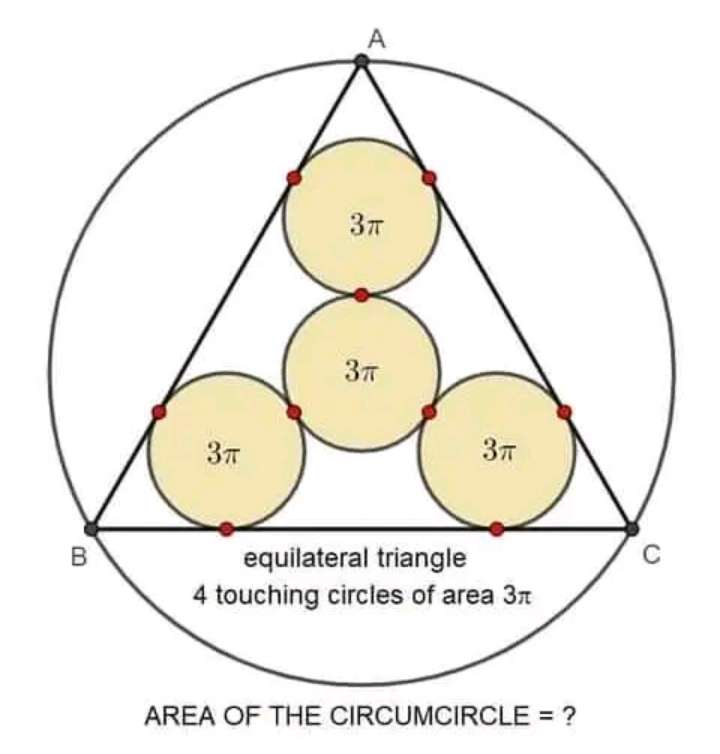
Calculating r, radius of the circumcircle.
2(√(3)) + 2(√(3))
r = 4√(3) units.
Therefore area of the circumcircle is;
π(4√(3))²
= 48π square units.
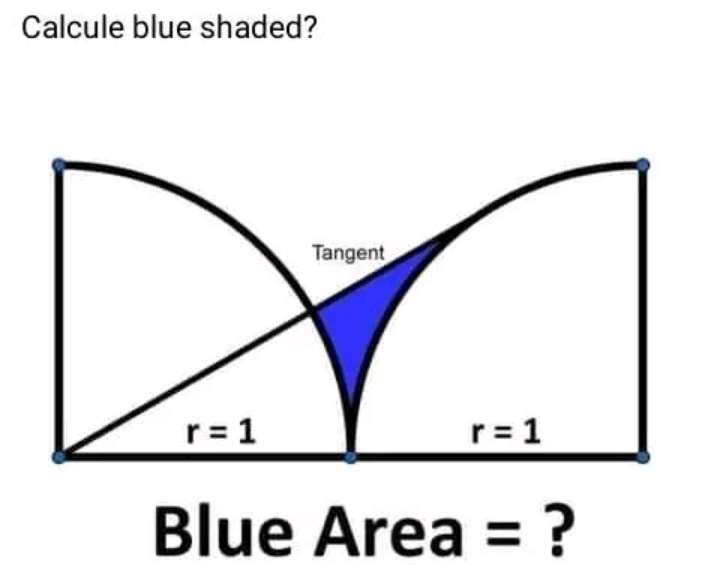
Area blue is;
Area triangle with height √(3) units and base 1 unit - Area sector with radius 1 unit and angle 60° - Area sector with radius 1 unit and angle 30°
= ½√(3) - (π/6) - (π/12)
= (6...
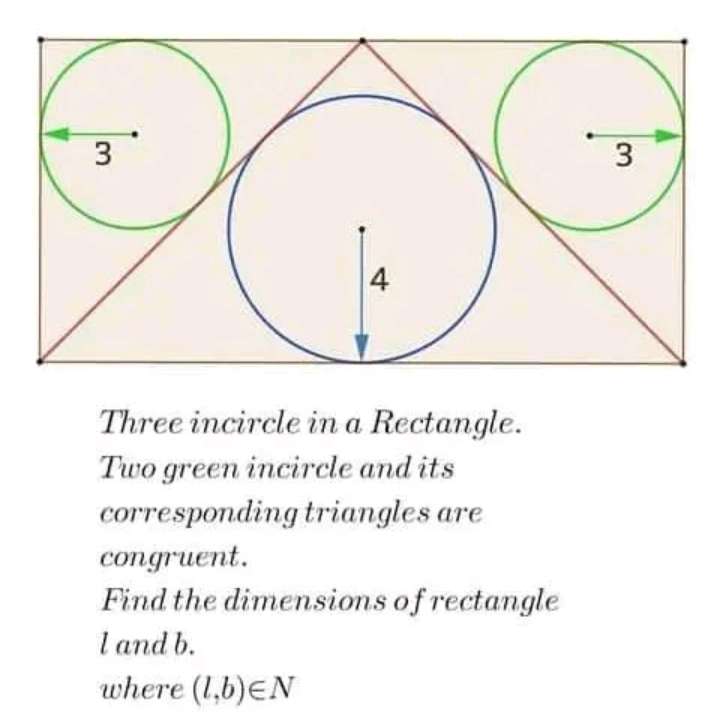
Let the width of the square be x.
Therefore the length of the square will be 2x.
Calculating x.
x² + x² = (2√(3²+3²)+2(3))²
2x² = (2√(18)+6)²
2x² = (6√(2)+6)²
2x² = 72+72√(2)+36
x² = 54+...
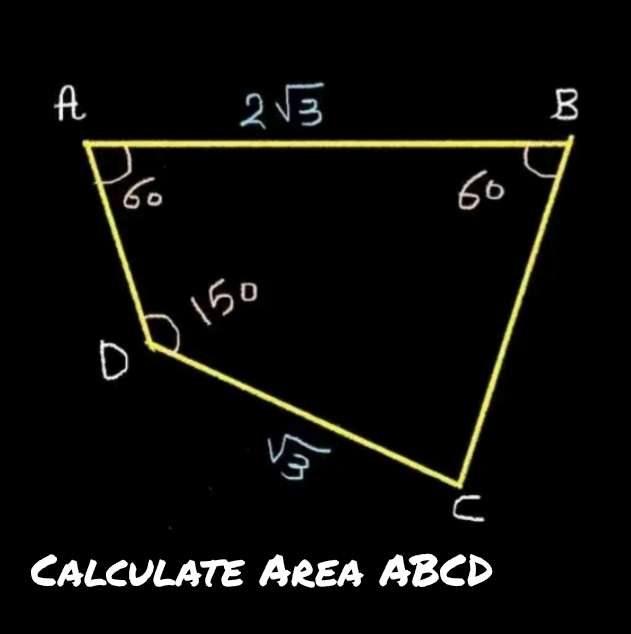
Area ABCD is;
½((5√(3)) square units.
Please, move the above question left/right to review the solution.
Thank you.