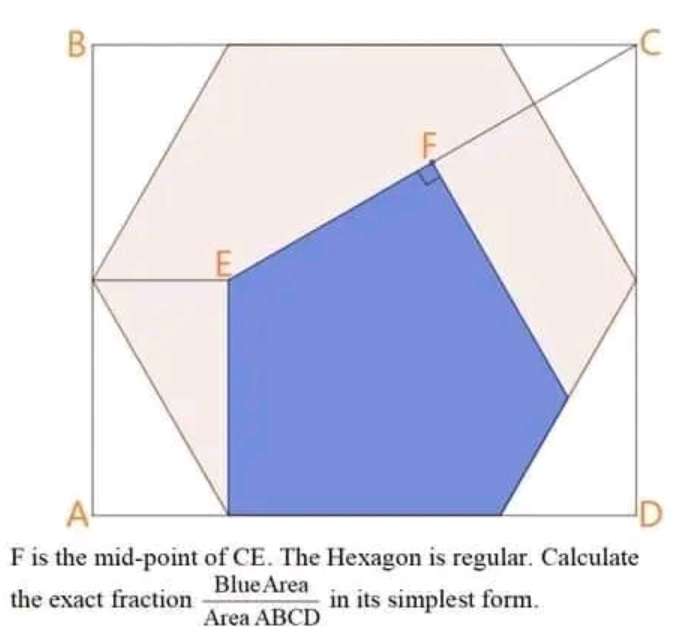
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
Let the single side length of the inscribed regular hexagon be 2 units.
Therefore;
Area rectangle ABCD is:
2√(3) * 4
= 8√(3) square units.
Area Blue will be;
Area rectangle with length 4 units and width 2√(3) units - Area trapezium with two parallel length sum (1+4) units and height √(3) units - Area rectangle with length √(3) units and width 1 unit - Area triangle with height √(3)sin(atan√(3)) units and base √(3)cos(atan√(3)) units - Area triangle with height √(3) units and base 1 unit - Area trapezium with two parallel length sum (2(√(3)sin(atan√(3)))+1-cos(atan√(3))) units and height (√(3)-√(3)cos(atan√(3)) units.
= 8√(3) - ½(5√(3)) - √(3) - ½(√(3)sin(atan√(3))*√(3)cos(atan√(3))) - ½(√(3)) - ½(2(√(3)sin(atan√(3)))+1-cos(atan√(3)))(√(3)-√(3)cos(atan√(3))
= 8√(3) - ½(5√(3)) - √(3) - (3√(3))/8 - ½(√(3)) - (7√(3))/8
= (64√(3)-20√(3)-8√(3)-3√(3)-4√(3)-7√(3))/8
= (64√(3)-42√(3))/8
= (22√(3))/8
= ¼(11√(3)) square units.
Therefore;
Area Blue ÷ Area Rectangle ABCD is;
¼(11√(3)) ÷ 8√(3)
= 11/32