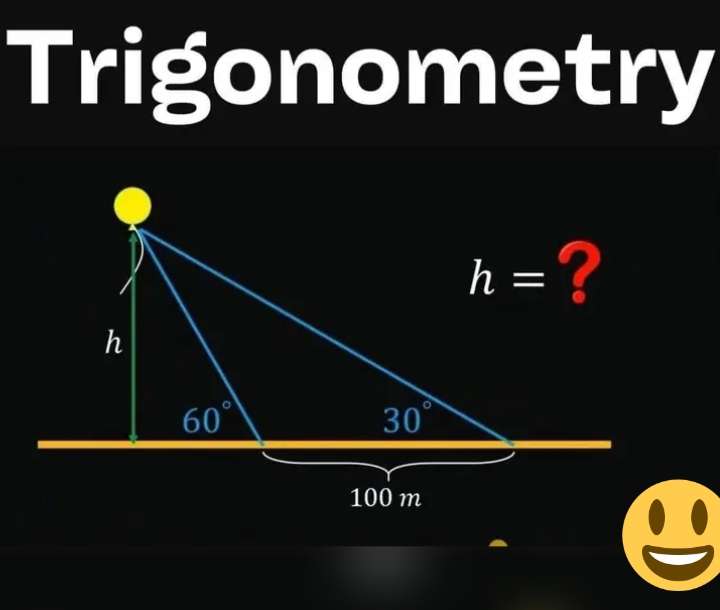
tan60 = h/a
a = ⅓√(3)h m.
b = 100+a
b = (100+⅓√(3)h) m.
tan30 = h/(100+⅓√(3)h)
√(3)h = (100+⅓√(3)h)
3√(3)h = 300+√(3)h
2√(3)h = 300
√(3)h = 150
h = 50√(3) m.
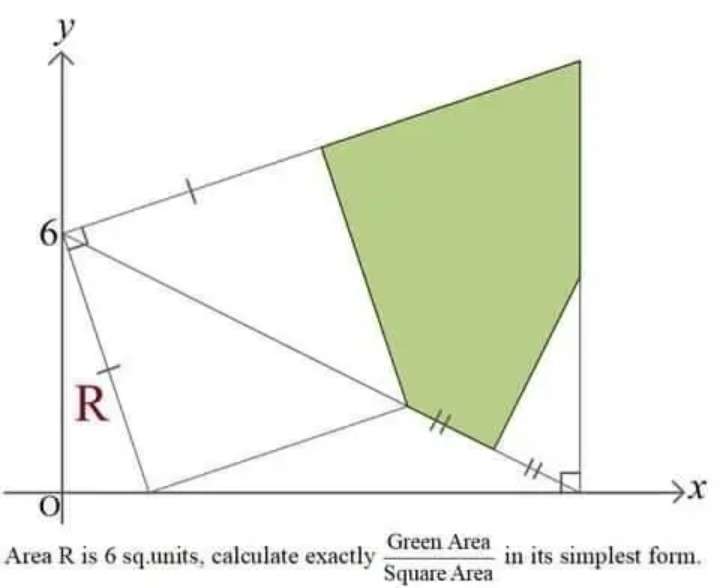
Sir Mike Ambrose is the author of the question.
Area Square is:
√(40)²
= 40 square units.
Area Green is;
Area triangle with two lengths 4√(10) units and 6√(5) units, and angle 45°, the...
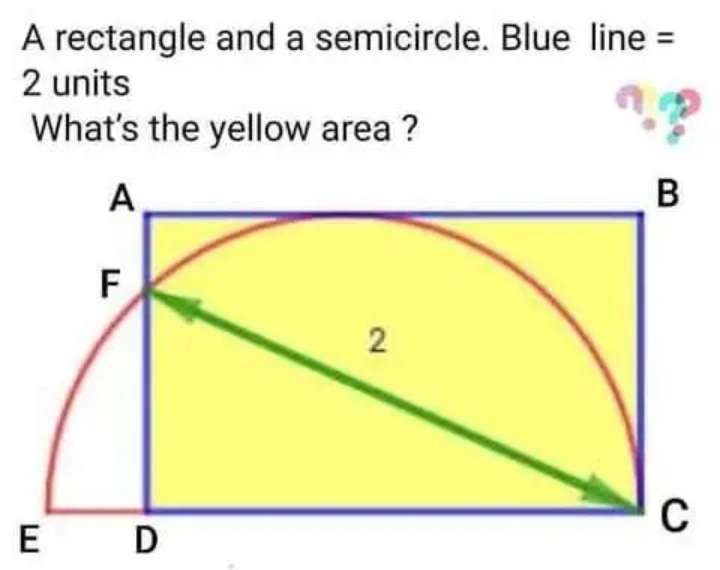
AD = BC = Width of Rectangle ABCD = Radius of the Semi Circle R = √(4-2√(2)) units.
AB = CD = Length of Rectangle ABCD = (2/√(4-2√(2))) units.
It implies;
Area Yellow (Rectangle ABCD) is;...
Please, move the above question left/right one time to review the solution.
Thank you.
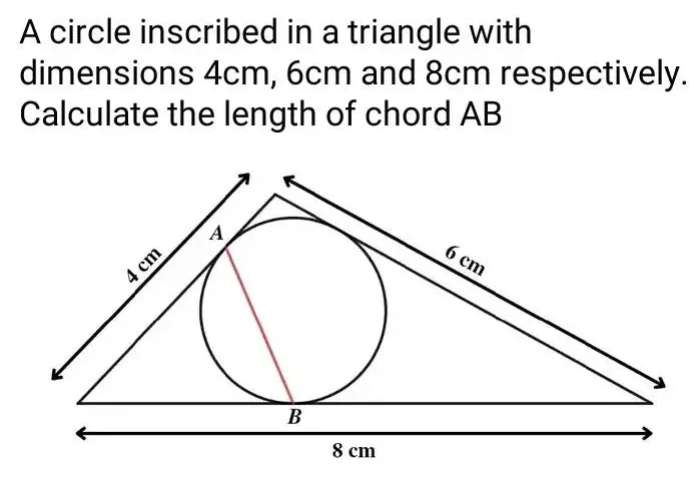
Length AB is;
2.37 cm to 2 decimal places.
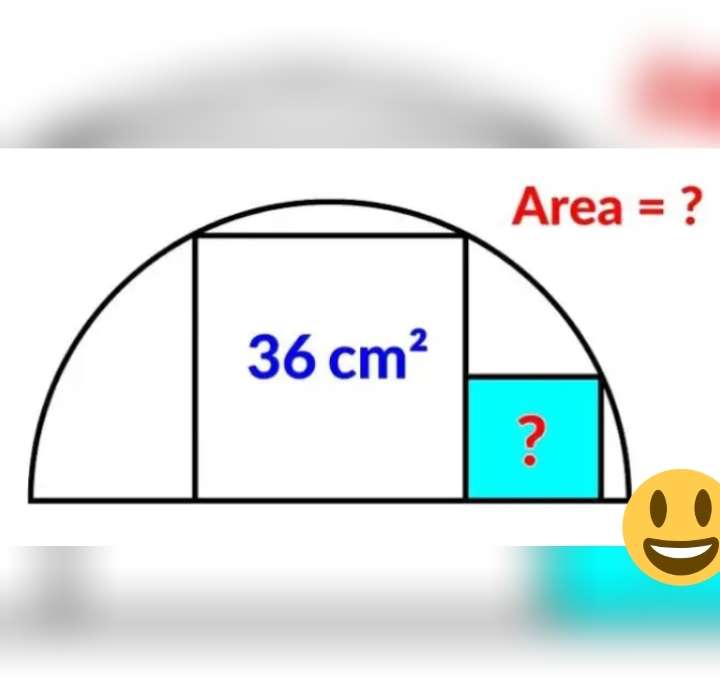
a² = 36
a = 6 cm.
a is the side length of the inscribed big square.
b² = a²+(0.5a)²
b² = 6²+(0.5*6)²
b² = 36+9
b = √(45)
b = 3√(5) cm.
b is the radius of the ascribed semi circle.
Let...
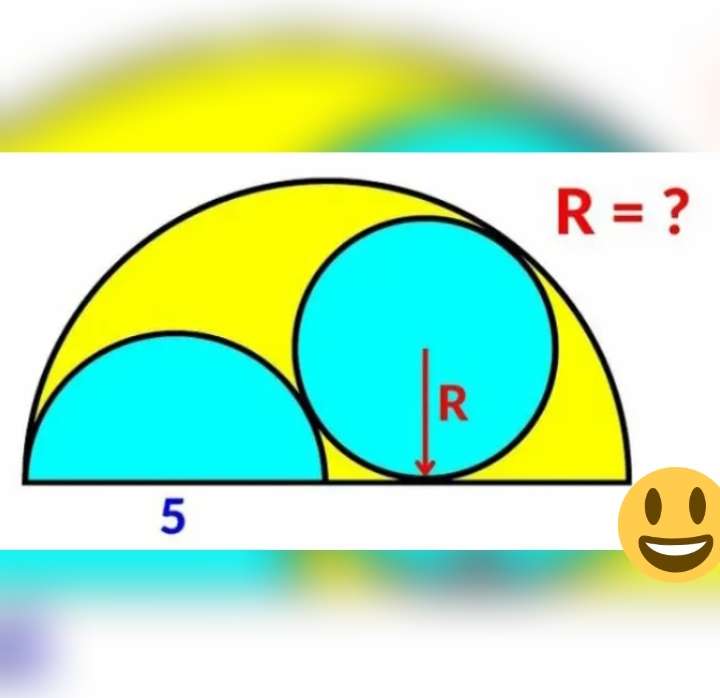
Notice.
Radius of the ascribed semi circle is 5 units.
a = (5-R) units.
(5-R)² = b²+R²
b² = 25-10R+R²-R²
b² = 25-10R
b = √(25-10R) units.
c = ½(5)+b
c = (2.5+√(25-10R)) units.
d...
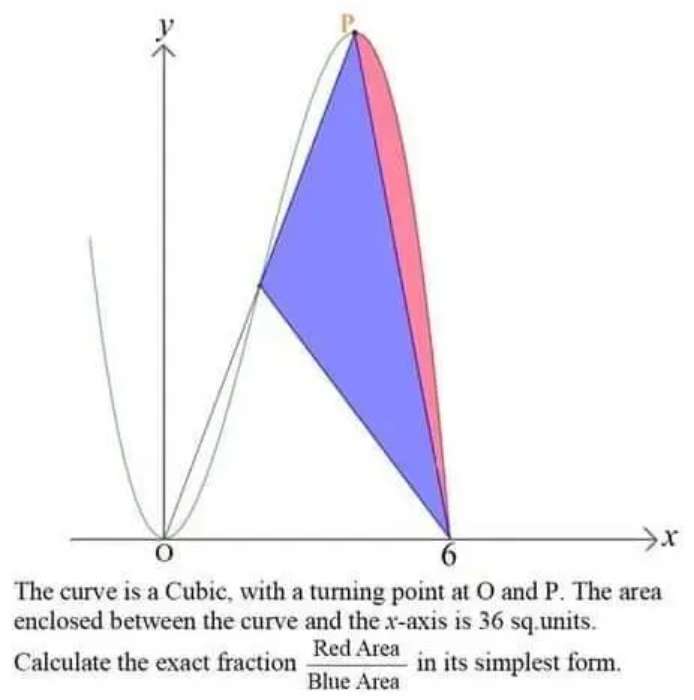
Sir Mike Ambrose is the author of the question.
Area of the curve is;
y = -⅓(x³)+2x²
Point p coordinate is;
(⅓(32), 4)
Therefore Area Red is;
Area under the curve at the points (4, 0)...
Please, move the above question right/left one time to review the solution.
Thank you.
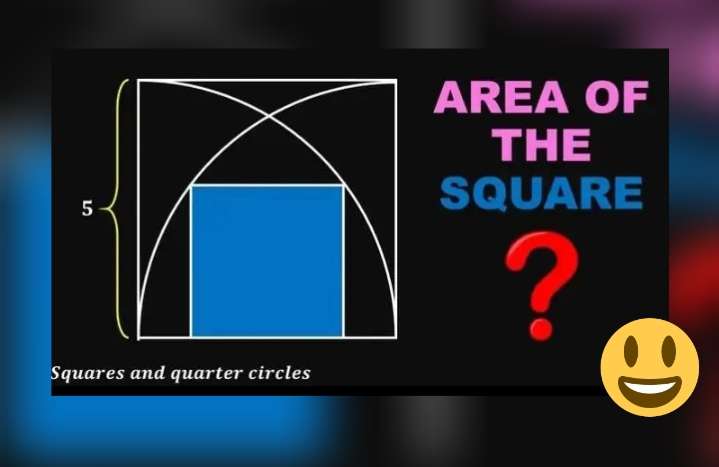
Area inscribed blue square is;
9 square units.
Please, move the above question left/right one time to review the solution.
Thank you.
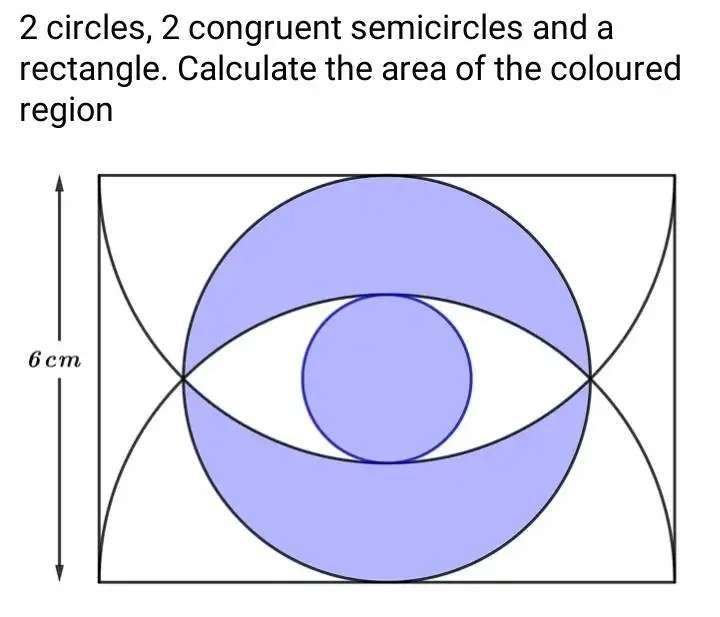
Coloured area region is;
22.85 cm² to 2 decimal places.
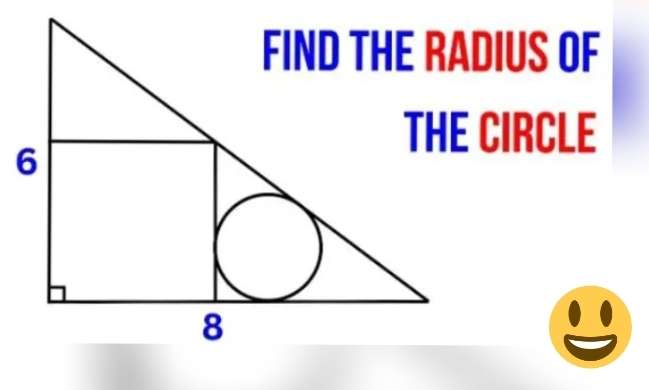
Let a be the side length of the inscribed square.
Calculating a.
b = (6-a) units.
Therefore;
6 - (6-a)
8 - a
Cross Multiply.
6a = 48-8a
14a = 48
7a = 24
a = (24/7) units.
Aga...