Mathematics Question and Solution
Notice!
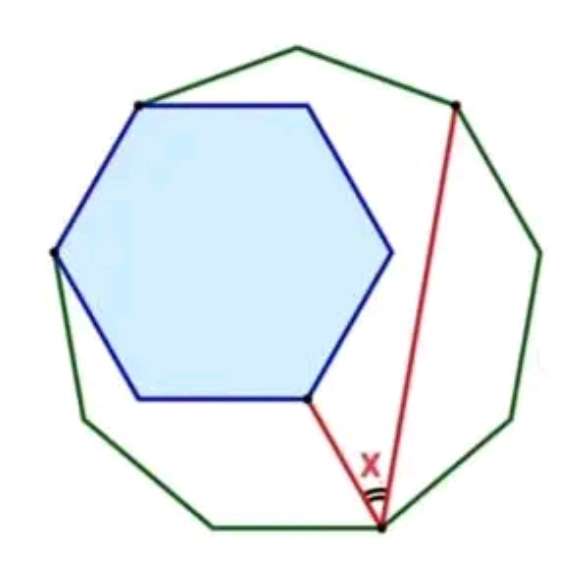
The ascribed polygon is a regular nonagon.
The inscribed polygon is a regular hexagon.
Calculating the required angle, x.
a = ⅙*180(6-2)
a = 120°
a is the single interior angle of the regular hexagon.
b = ⅑*180(9-2)
b = 140°
b is the single interior angle of the regular nonagon.
c = ½(360-140+140)
c = ½(360-280)
c = ½(80)
c = 40°
d = ⅕*180(5-2)
d =108°
d is the single interior angle of the regular pentagon.
e = 5d
e = 540°
e is the sum of interior angles of a regular pentagon.
It implies;
f = ½(540-3(140))
f = ½(540-420)
f = ½(120)
f = 60°
Therefore, the required angle, x is;
x+c+f = 140
x+40+60 = 140
x = 140-60-40
x = 140-100
x = 40°