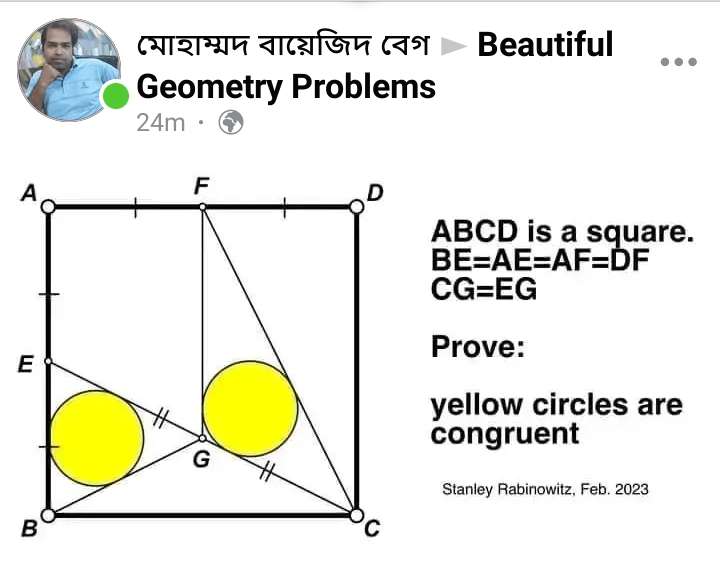
Mathematics Question and Solution
Let the square side be 2 units.
Calculating the radius of the yellow circle inscribed triangle BGE.
Let it be x.
(0.5)²+1 = a²
a = ½√(5) units.
a is EG = BG.
x+2(½√(5))x = 1
(1+√(5))x = 1
x = 1/(1+√(5)) units.
Calculating the radius of the yellow circle inscribed triangle CGF.
Let it be y.
b² = 1+2²
b = √(5) units.
b is CF.
CG = ½(b)
CG = ½√(5) units.
FG = 1+½
FG = (3/2) units.
FG = 1.5 units.
Therefore;
√(5)y+½√(5)y+½(3y) = (2-½)
√(5)y+½√(5)y+½(3y) = (3/2)
2√(5)y+√(5)y+3y = 3
3√(5)y+3y = 3
(√(5)+1)y = 1
y = 1/(√(5)+1) units.
Notice;
x = y (equal radius)
Therefore the two yellow Inscribed circles are congruent.
Proved.