Mathematics Question and Solution
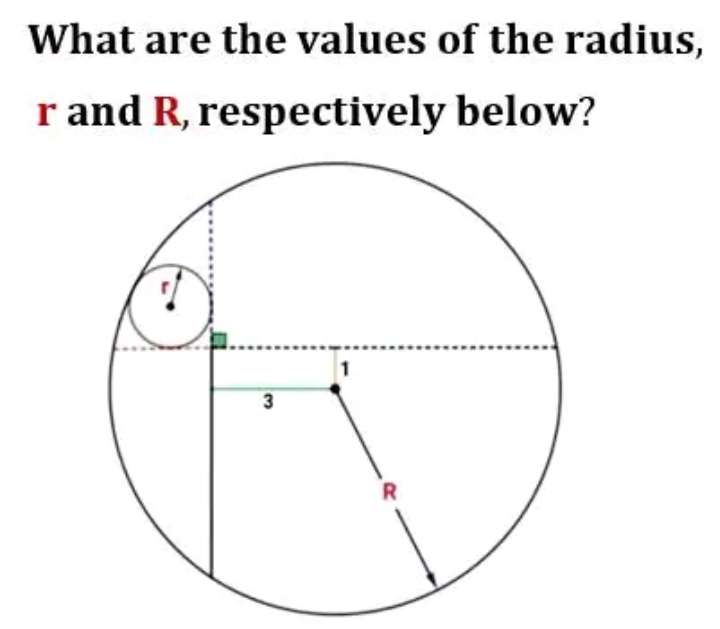
Calculating R.
a²+3² = R²
a = √(R²-9) units.
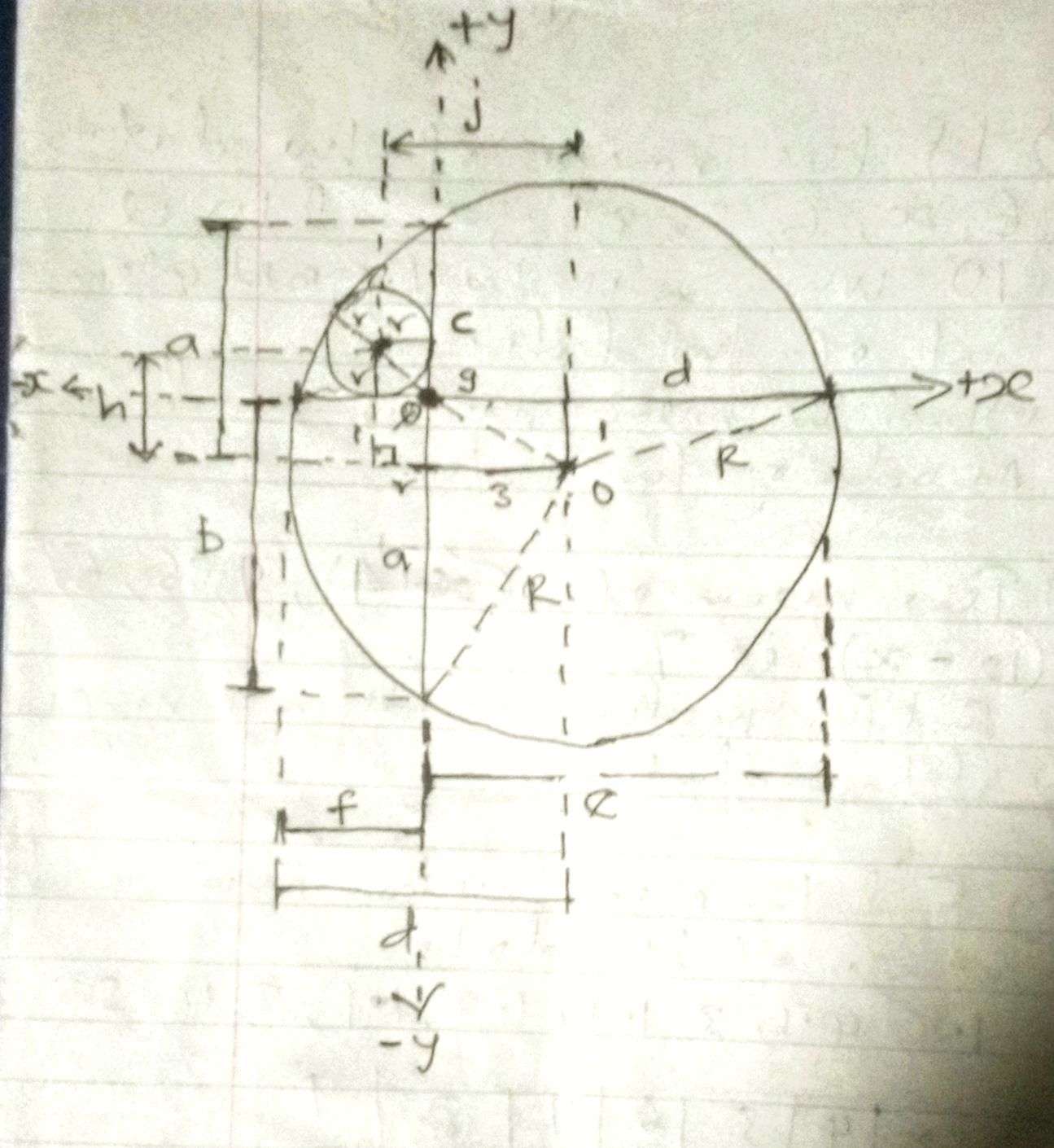
b = 1+a
b = (1+√(R²-9)) units.
c = a-1
c = (√(R²-9)-1) units.
d²+1² = R²
d = √(R²-1) units.
e = 3+d
e = (3+√(R²-1)) units.
f = d-3
f = (√(R²-1)-3) units.
Therefore;
(√(R²-1)-3)(3+√(R²-1)) = (1+√(R²-9))(√(R²-9)-1)
√(R²-1)-9 = √(R²-9)-1
√(R²-1)-8 = √(R²-9)
R²-1-16√(R²-1)+64 = R²-9
16√(R²-1) = 72
2√(R²-1) = 9
4(R²-1) = 81
4R² = 85
R = √(85/4)
R = ½√(85) units.
R = 4.6097722286 units.
R is the radius of the ascribed big circle.
Calculating r, radius of the inscribed small circle.
g = (½√(85)-r) units.
h = (1+r) units.
j = (3+r)
It implies;
(½√(85)-r)² = (1+r)²+(3+r)²
¼(85)-√(85)r+r² = 1+2r+r²+9+6r+r²
¼(85)-√(85)r = r²+8r+10
r²+(8+√(85))r+10-¼(85) = 0
4r²+(32+4√(85))r-45 = 0
Resolving the above quadratic equation via completing the square approach to get r, radius of the small inscribed circle.
r²+(8+√(85))r = ¼(45)
(r+½(8+√(85)))² = ¼(45)+(½(8+√(85)))²
(r+½(8+√(85)))² = 85.3781778292
r+8.6097722286 = ±√(85.3781778292)
r = -8.6097722286±9.2400312678
It implies;
r = 9.2400312678-8.6097722286
r = 0.6302590392 units.
Again, r is the radius of the small inscribed circle.