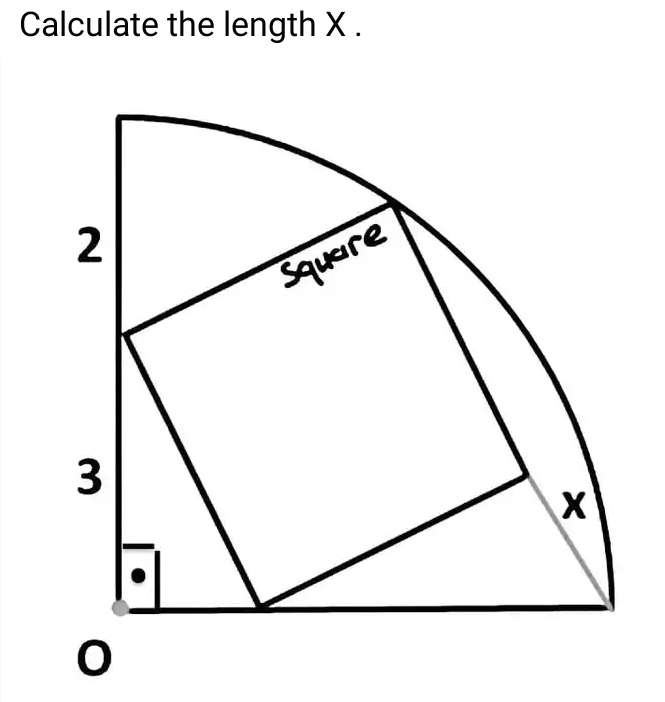
Mathematics Question and Solution
Radius of the quarter circle is (2+3) = 5 units.
Let a be the side length of the inscribed square.
b²+3² = a²
b = √(a²-9) units.
c = 3+b
c = (3+√(a²-9)) units.
Calculating a.
(3+√(a²-9))²+3² = 5²
9+6√(a²-9)+a²-9+9 = 25
9+6√(a²-9)+a² = 25
6√(a²-9) = 16-a²
36(a²-9) = (16-a²)²
36a²-324 = 256-32a²+a⁴
a⁴-68a²+580 = 0
It implies;
a = √(10) units
a = 3.1622776602 units.
Again, a is the side length of the inscribed square.
Recall.
b = √(a²-9) units
And a = √(10) units.
b = √(√(10)²-9)
b = 1 unit.
d = 5-b
d = 4 units.
tane = 1/3
e = atan(⅓)°
Therefore, the required length, x is;
x² = √(10)²+4²-2*4√(10)cos(atan(⅓))
x = 1.4142135624 units.
x = √(2) units.