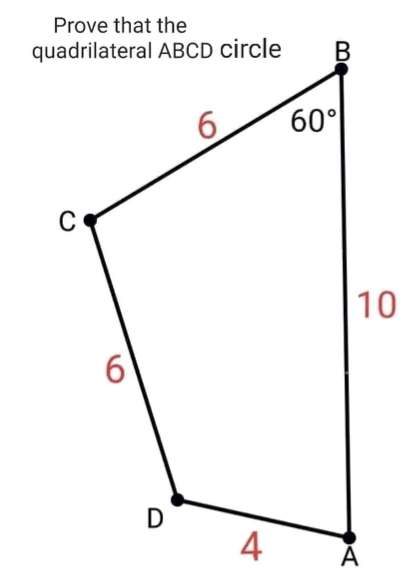
Mathematics Question and Solution
Showing that quadrilateral ABCD is cyclic.
Notice!
For quadrilateral ABCD to be cyclic;
Angle ADC will equal 2 times angle ABC.
Angle ADC = 2(Angle ABC)
It implies;
Since Angle ABC = 60°
Angle ADC must equal 2(60°) = 120°
The working!
a² = 10²+6²-2*10*6cos60
a = 2√(19) units.
a = 8.7177978871 units.
a is AC.
Therefore, calculate angle ADC. Let it be b.
(2√(19))² = 6²+4²-2*6*4cosb
76 = 52-48cosb
48cosb = 52-76
cosb = -24/48
b = acos(-1/2)
b = 120°
b is angle ADC.
Since Angle ADC, 120° is twice Angle ABC, 60°. It implies that quadrilateral ABCD is cyclic.