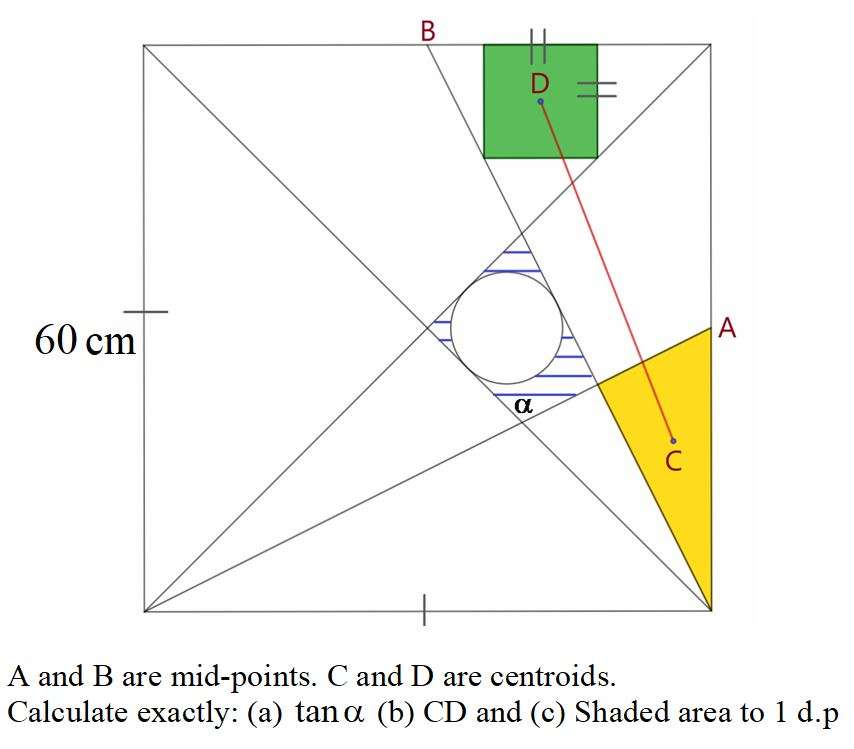
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
a = atan(2)°
b = (45+atan(½))°
(a) Calculating Alpha.
Let alpha be c.
c = 180-b
c = 180-45-atan(½)
c = (135-atan(½))°
Or
c = 180-(135-atan2)
c = (45+atan2)°
Let the green square side be d.
Calculating d.
2d+½(d) = 30
d = 12 cm.
e = atan(⅓)°
f² = 18²+6²
f = 6√(10) cm.
g² = 18²+56²
g = 2√(865) cm.
h² = 42²+54²
h = 6√(130) cm.
i = 90-atan(9/28)-atan(7/9)
(b) Calculating Length CD exactly in cm.
Let it be j.
j² = (2√(865))²+(6√(130))²-24√(865)*√(130)cos(90-atan(9/28)-atan(7/9))
= 2√(373) cm.
(c) Calculating shaded area to 1 decimal place cm².
k = ½(60√(2))
k = 30√(2) cm.
l = (12/sin(135-atan2))=(l/sin(atan(2)))
l = 8√(2) cm.
m = 30√(2)-8√(2)-12√(2)
m = 10√(2) cm.
n = 30√(2)tan(45-atan(½))
n = 10√(2) cm.
o = 12√(5)tan(45-atan(½))
o = 8.94427191 cm.
p = 24√(5)tan(45-atan(½))
p = 17.88854382 cm.
Calculating q, radius of the inscribed circle.
tan(0.5(135-atan2)) = q/(10√(2)-q)
q = 5.92359147246 cm.
Therefore;
Shaded area is;
Area triangle with height 10√(2) units and base 10√(2) units + Area triangle with height 17.88854382 units and base 8.94427191 units - Area circle with radius 5.92359147246 units.
= ½(10√(2))² + ½*17.88854382*8.94427191 - π(5.92359147246)²
= 100 + 80 - 110.23514334814
= 69.76485665186
≈ 69.8 cm²
Therefore;
(a) is (45+atan2)°
(b) is 2√(373) cm.
(c) is 69.8 cm².