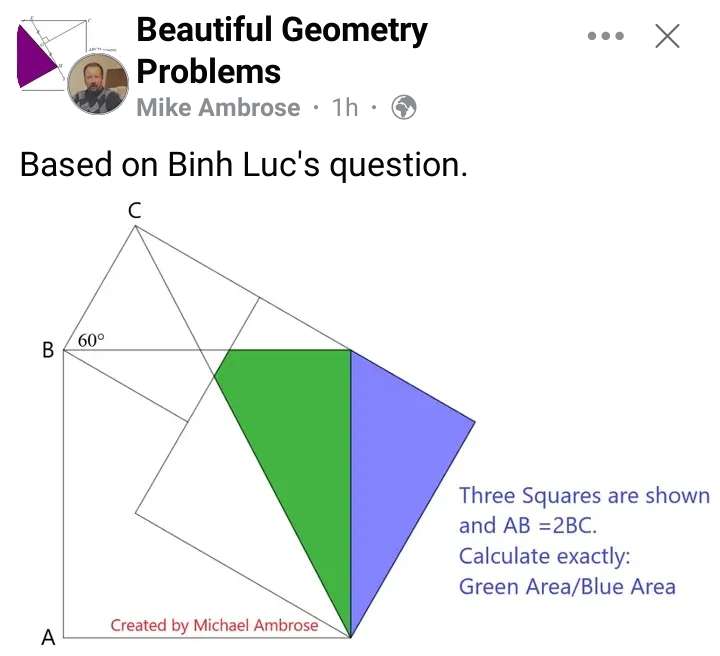
Mathematics Question and Solution
Let BC be 1 unit.
tan60 = a/1
a = √(3) units.
b² = √(3)²+1
b² = 4
b = 2 units.
b is AB.
Area Blue is;
½*1*√(3)
= ½√(3) square units.
Calculating Area Green.
tanc = √(3)/(√(3)+1)
c = atan(½(3-√(3)))°
(½(3-√(3))) = d/1
d = ½(3-√(3)) units.
e = (√(3)-1) units.
tan30 = f/(√(3)-1)
f = ⅓(3-√(3)) units.
It implies;
Area Green is;
Area trapezoid with parallel sides (½(3-√(3))) units and √(3) units respectively, and height √(3) units - Area Blue - Area triangle with height (√(3)-1) units and base (⅓(3-√(3))) units.
(½*((½(3-√(3)))+√(3))*√(3)) - (½√(3)) - (½*(√(3)-1)*(⅓(3-√(3))))
= ¼(3√(3)+3)-½√(3)-⅙(3√(3)-3-3+√(3))
= ¼(3√(3)+3)-½√(3)-⅙(4√(3)-6)
= (9√(3)+9-6√(3)-8√(3)+12)/12
= (9√(3)-14√(3)+21)/12
= (21-5√(3))/12 square units.
Therefore;
Area Green ÷ Area Blue Exactly is;
((21-5√(3))/12)÷½√(3)
= (21-5√(3))/(6√(3))
= (21√(3)-15)/18
= ⅙(7√(3)-5)