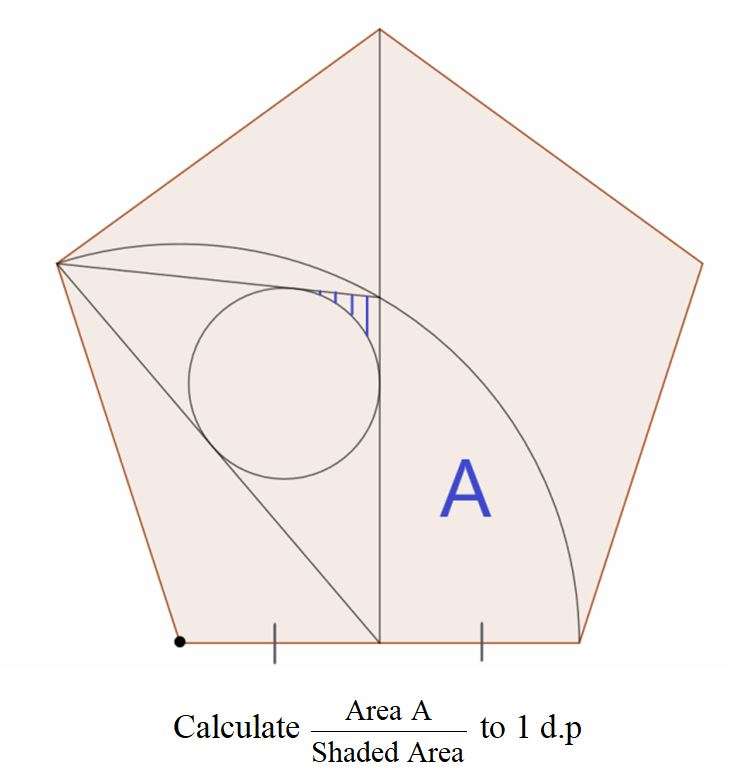
Mathematics Question and Solution
Let the side length of the regular pentagon be 2 units.
a² = 2²-1²
a = √(3) units.
b² = 5-4cos108
b = 2.49721204096 units.
(2.49721204096/sin108) = (2/sinc)
c = 49.61382244056°
d = 90-c
d = 40.38617755944°
e² = 3+2.49721204096²-2√(3)*2.49721204096cos40.38617755944
e = 1.62694657231 units.
(1.62694657231/sin40.38617755944) = (√(3)/sinf)
f = 43.61382244075°
g = 180-e-f
g = 96°
Let the radius of the inscribed circle be r.
Calculating r.
r(√(3)+1.62694657231+2.49721204096) = (1.62694657231*√(3)sin96)
r = 0.47855479125 units.
h = 90-½(96)
h = 42°
tan42 = i/r
i = 0.43089266946 units.
cos42 = r/j
j = 0.64395899002 units.
It implies;
Area Shaded is;
2((½*0.43089266946*0.47855479125) - (42π*0.47855479125²/360))
= 2(0.10310287574 - 0.08393826725)
= 2(0.01916460849)
= 0.03832921698 square units.
Area A is,
(60π*4/360) - (0.5*√3)
= 2.09439510239 - 0.86602540378
= 1.22836969861 square units.
Therefore;
Area A ÷ Area Shaded to 1 decimal place is;
1.22836969861 ÷ 0.03832921698
= 32.04786832057
≈ 32