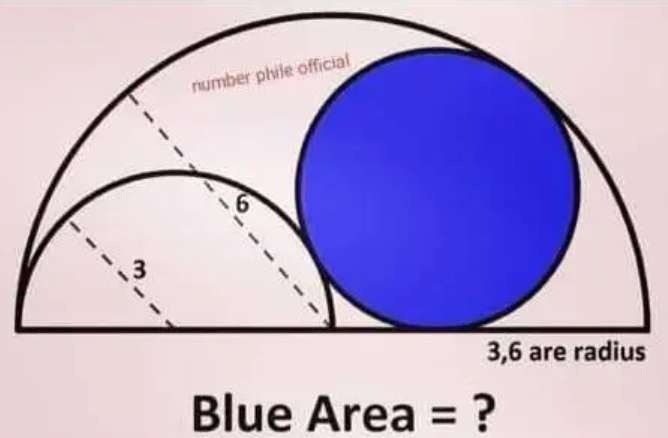
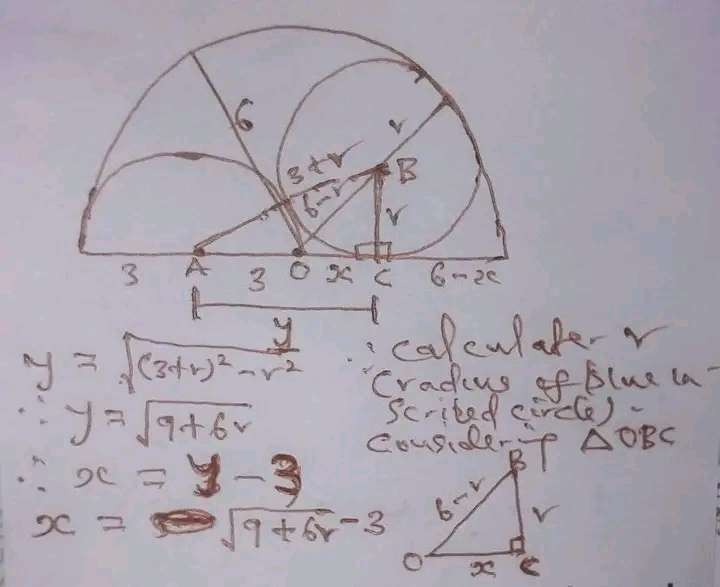Mathematics Question and Solution
Calculating r, the radius of the blue inscribed circle.
Therefore;
Consider triangle OBC.
(6-r)² = r² + x², and x = √(9+6r) - 3
It implies;
(6-r)² = r² + (√(9+6r)-3)²
36-12r+r²=r²+9-6√(9+6r)+(9+6r)
36-12r=9-6√(9+6r)+9+6r
6√(9+6r) = 18r-18
√(9+6r) = 3r-3
9+6r = (3r-3)²
9+6r = 9r²-18r+9
24r = 9r²
Therefore r, radius of the blue inscribed circle is;
r ≠ 0
r = (8/3) units.
Therefore area inscribed blue circle is;
π(8/3)²
= 64π/9 square units.