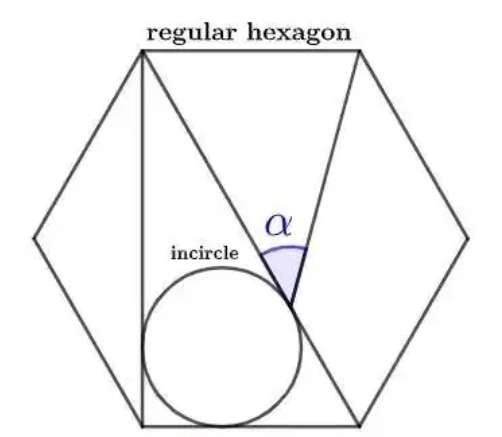
Mathematics Question and Solution
Let the side length of the ascribed regular hexagon be 1 unit.
a = ⅙*180(6-2)
a = 120°
a is the single interior angle of the ascribed regular hexagon.
b = ¼(a)
b = 30°
d = (1-c)
c is the radius of the inscribed circle.
Calculating c.
tan30 = c/(1-c)
√(3)c = 1-c
(1+√(3))c = 1
c = 1/(1+√(3)) units.
c = 0.3660254038 units.
Recall.
d = 1-c
d = 0.6339745962 units.
e² = 2-2cos120
e = √(3) units.
f² = √(3)²+0.6339745962²-2√(3)*0.6339745962cos30
f = 1.2247448714 units.
Calculating the required angle, alpha.
Let it be g.
(1.2247448714/sin30) = (√(3)/sing)
g = 45°
Again, g is the required angle, alpha.