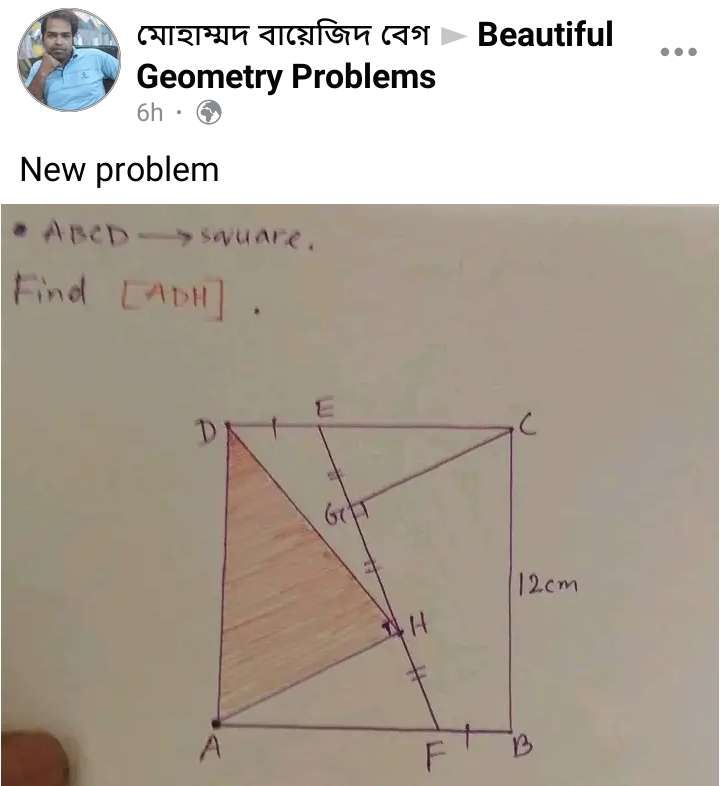
Mathematics Question and Solution
Let DE = BF = a.
Let EG = GH = HF = b.
(3b)² = 12²+(12-2a)
9b² = 144+144-48a+4a²
b² = ⅑(288-48a+4a²) ----- (1).
CF = √(144+a²)
(CG)² = (12-a)²-b²
CG = √((12-a)²-b²)
Therefore;
(144+a²) = 4b²+((12-a)²-b²)
144+a² = 4b²+144-24a+a²-b²
24a = 3b²
b² = 8a ----- (2).
Equating (1) and (2).
⅑(288-48a+4a²) = 8a
4a²-120a+288 = 0
a²-30a+72 = 0
(a-15)² = -72+225
a = 15±√(153)
a ≠ 15+3√(17)
a = 15-3√(17) cm.
a = 2.63068312315 cm.
AF = 12-2.63068312315
AF = 9.36931687685 cm.
HF = √(8a)
HF = √(8*2.63068312315)
HF = 4.58753364949 cm.
AH = √(9.36931687685²-4.58753364949²)
AH = 8.16937168659 cm.
sinc = 4.58753364949/9.36931687685
c = 29.31651111271°
Where c is angle FAH.
Angle DAH = 90-29.31651111271
= 60.68348888729°
It implies;
Area triangle ADH is;
0.5*12*8.16937168659sin60.68348888729
= 42.73863375368 cm²