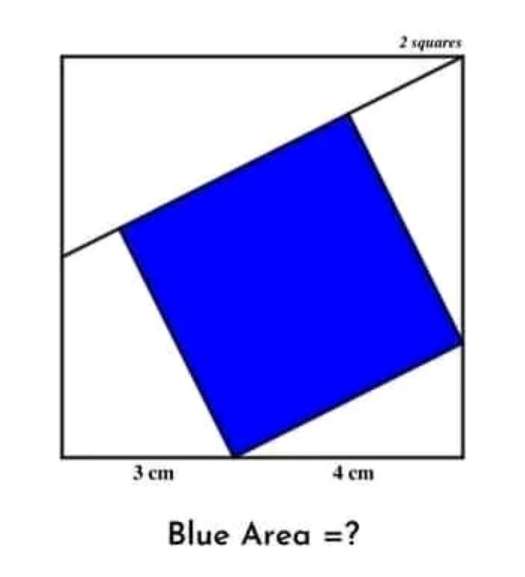
Let x be the single side length of the square.
Therefore;
x²=28-4√(x²-16) via similar triangle.
16(x²-16)=(28-x²)²
16x²-256=784-56x²+x⁴
x⁴-72x²+1040=0
Let x²(blue area) = P
Therefore;
P...
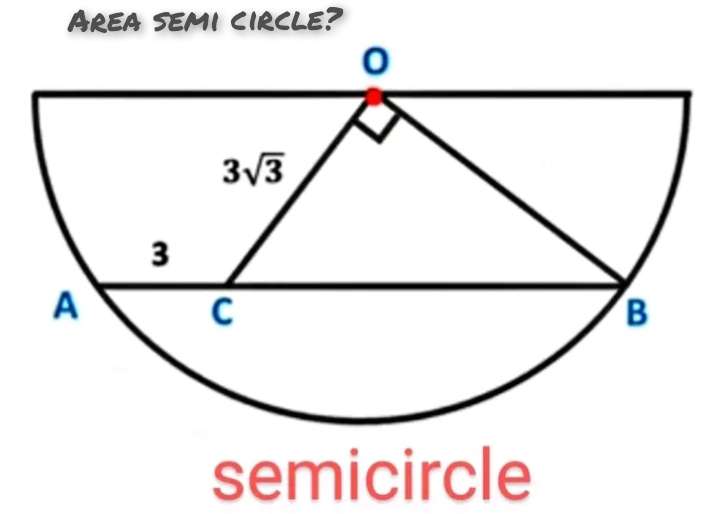
Let a be the radius of the half circle.
b² = (3√(3))²+a²
b = √(27+a²) units.
cosc = 3√(3)/√(27+a²) --- (1).
a² = 3²+(3√(3))²-2*3*3√(3)cosc
a² = 36+18√(3)cosc --- (2).
Substituting (1)...
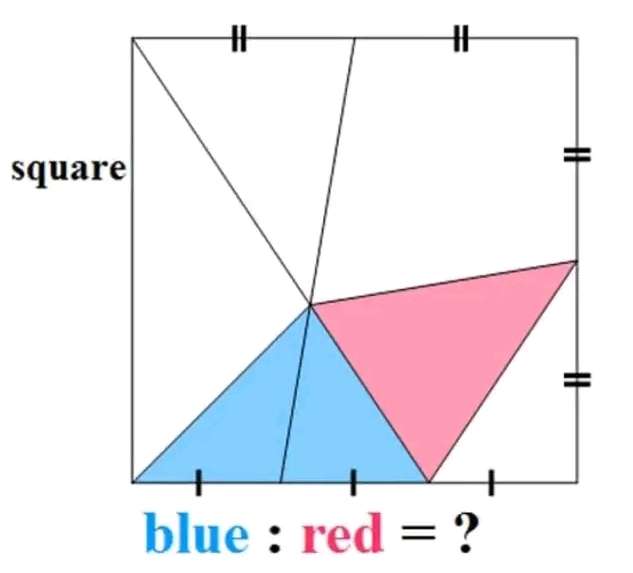
Let the square side length be 3 units.
tana = (3/2)
a = atan(3/2)°
tanb = 1.5/1
b = atan(3/2)°
c = 180-45-a
c = (135-atan(3/2))°
It implies;
(2/sin(135-atan(3/2))) = (d/sin(atan(3/2)))
d = 1.69...
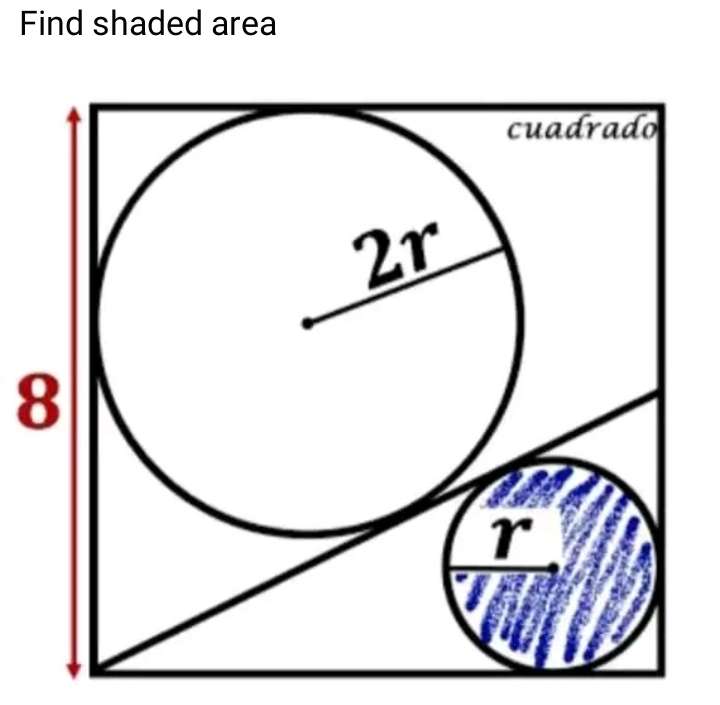
a = (8-2r) units.
Observing similar plane shape (right-angled) side length ratios.
r - 2r
b - (8-2r)
Cross Multiply.
2b = (8-2r)
b = (4-r) units.
c = r+b
c = r+(4-r)
c = 4 units.
tand = 8/4
d =...
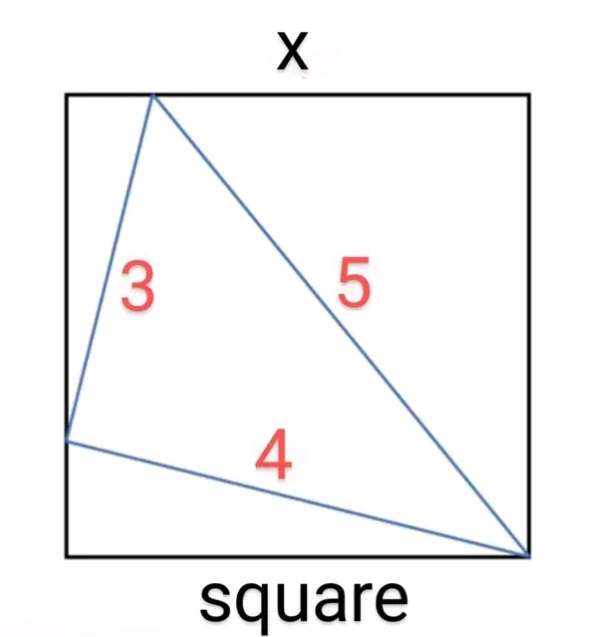
5² = x²+a²
a = √(25-x²) units.
b = x-a
b = (x-√(25-x²)) units.
c² = 4²-x²
c = √(16-x²) units.
Calculating x, the ascribed square side length.
Observing similar plane shape (right-angl...
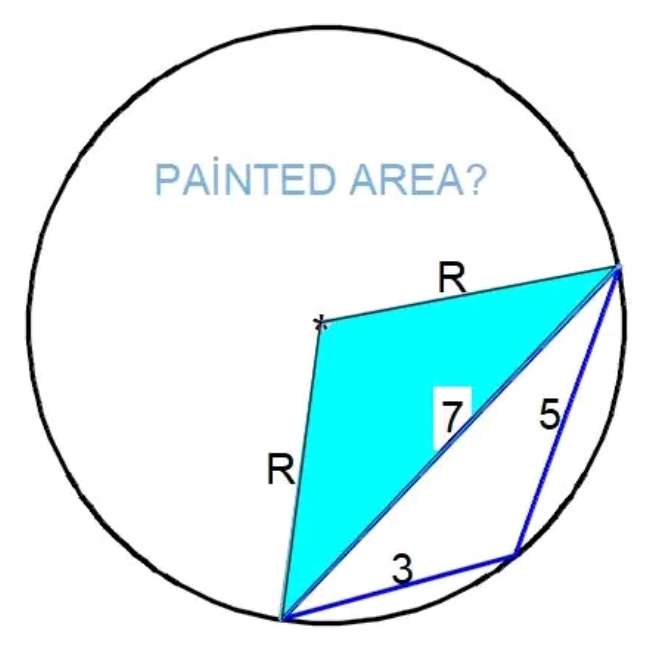
7² = 3²+5²-2*3*5cosa
30cosa = 34-49
cosa = (-15)/30
a = acos(-½)
a = 120°
b = 2a
b = 240°
c = 360-b
c = 120°
tan60 = 3.5/d
d = 3.5/√(3)
d = ⅓(3.5√(3))
d = ⅙(7√(3)) units.
There...
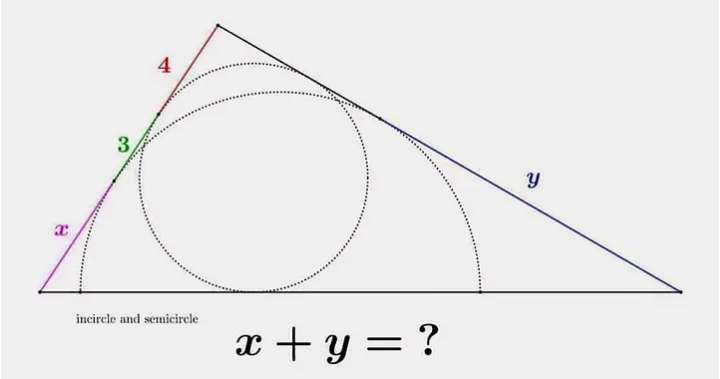
Notice!
Radius, a of the inscribed circle is 4 units.
Radius, b of the inscribed semi circle is 7 units.
3²+4² = c²
c = √(25)
c = 5 units.
d² = 5²+4²
d = √(41) units.
tane = 3/4
e...
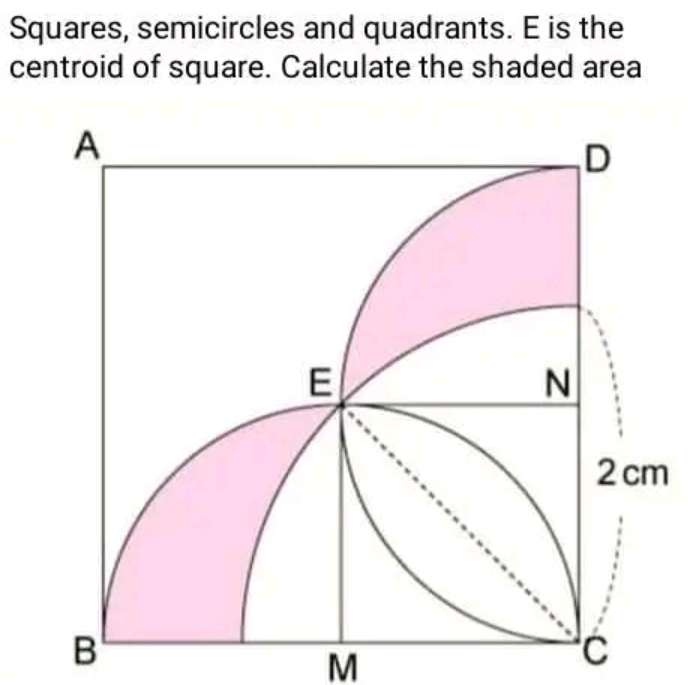
Shaded area will be;
Area semi circle of radius √(2) cm - area quarter circle of radius 2 cm + area square of single side length √(2) cm.
= ½(√(2))²π - ¼(2²)π + (√(2))²
= π-π+2
= 2 cm²
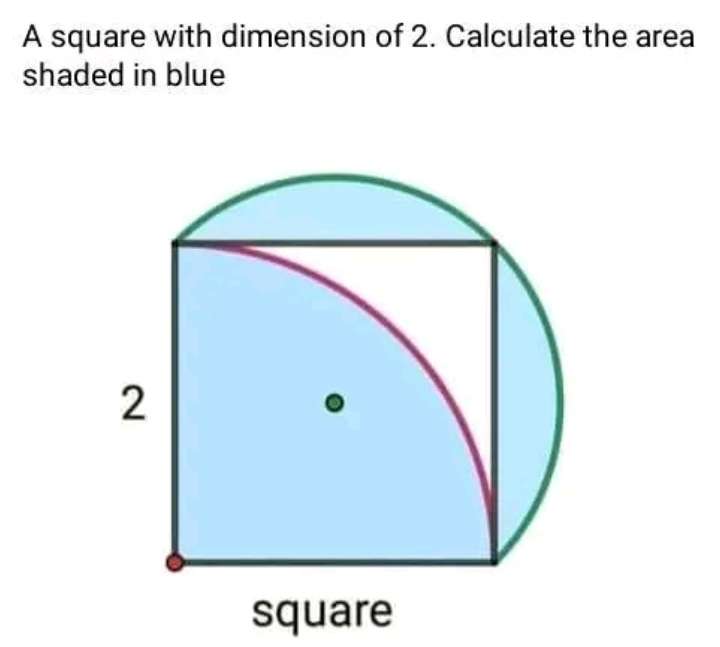
Shaded area will be;
Area quarter circle of radius 2 unit + 2(area quarter circle of radius √(2) unit - area triangle of height and base √(2) unit respectively).
= ¼(4π) + 2(¼(2π) - ½(2))
= π...
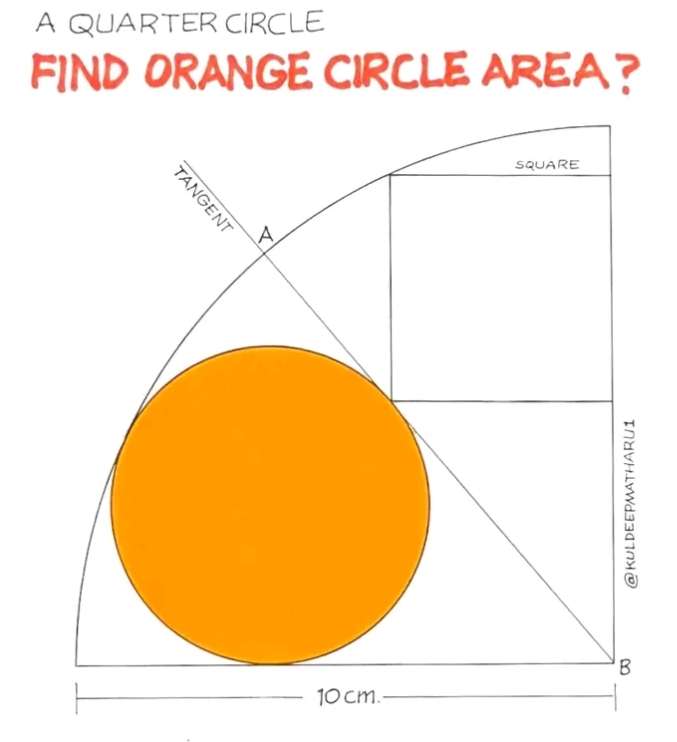
Let the inscribed square side be a.
b² = 2a²
b = √(2)a cm.
b is the diagonal of the inscribed square.
c = 90+45
c = 135°
It implies, calculating a, the inscribed square side length.
1...