
Calculating Area Blue.
a = ⅙*180(6-2)
a = 120°
a is the single interior angle of the regular hexagon.
sin30 = b/5
b = 2.5 c.
c = 2b+5
c = 10 cm.
d = ½(60)
d = 30°
sin60 = e/5
2e = 5√(3)
e = ½(5...
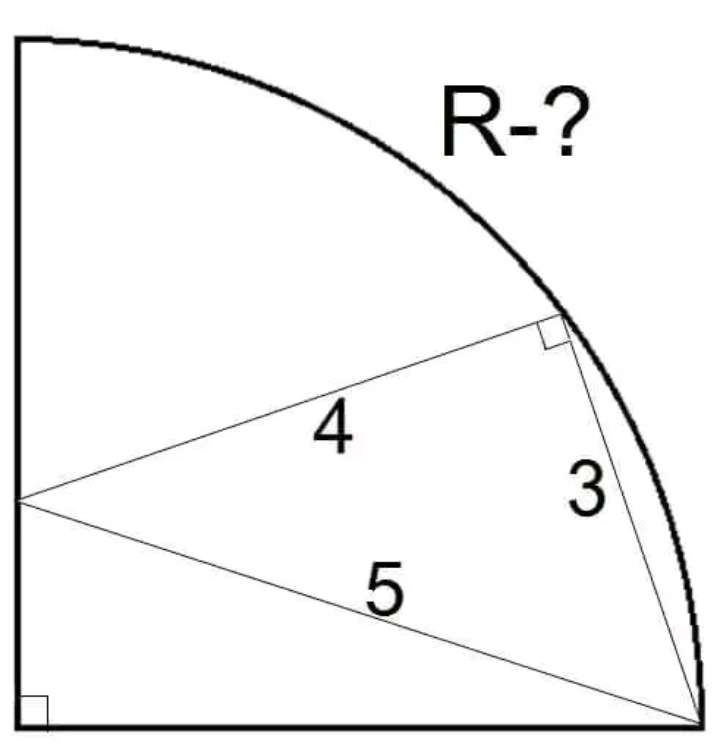
tana = 3/4
a = atan(3/4)°
b = ½(180-a)
b = ½(180-atan(3/4))
b = 71.5650511771°
Therefore, r, radius of the quarter circle is;
sin71.5650511771 = r/5
r = 4.7434164903 units.
Or
c = 4+5...
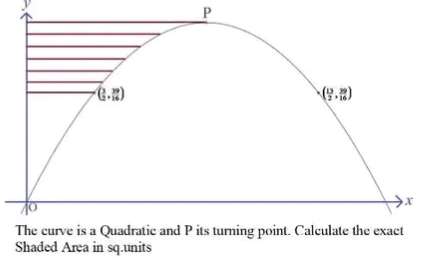
Sir Mike Ambrose is the author of the question.
Equation of the curve is;
y = 2x-¼(x²)
The vertex coordinate (maximum turning point) is at;
(4, 4)
Therefore;
Shaded Area in square units is;
Area...
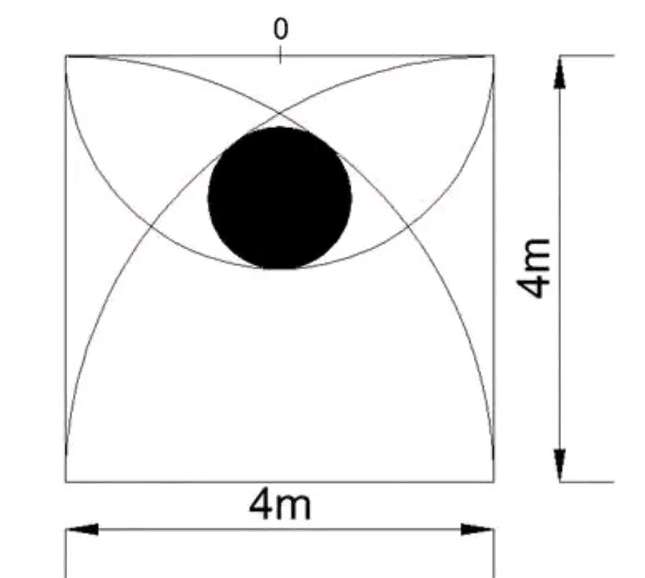
Calculating Area of the inscribed black circle.
Let a be the radius of the inscribed black circle.
b = (2+a) units.
c = (4-a) units.
It implies;
Calculating a.
(4-a)² = (2+a)²+2²
16-8a+a² = 4...
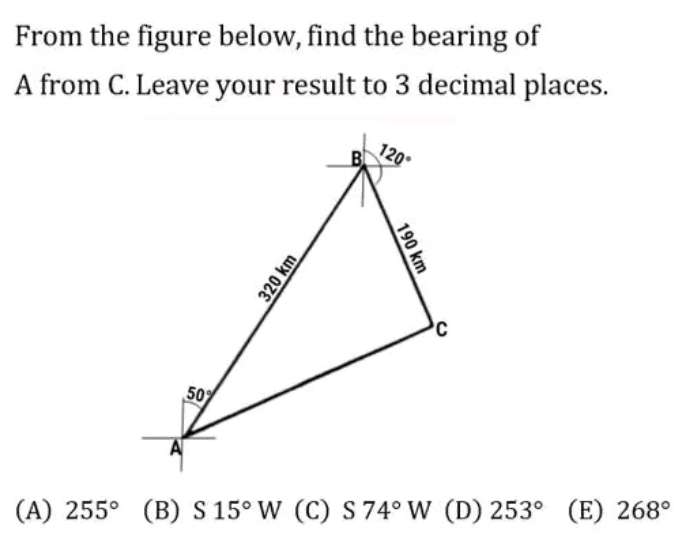
a = 180-120+50
a = 110°
a is angle ABC.
b² = 320²+190²-2*320*190cos110
b = 424.3697084246 km.
(424.3697084246/sin110) = (320/sinc)
c = 45.1198323317°
d = 360-60-c
d = 254.8801676683°
d ≈ 254.880°...
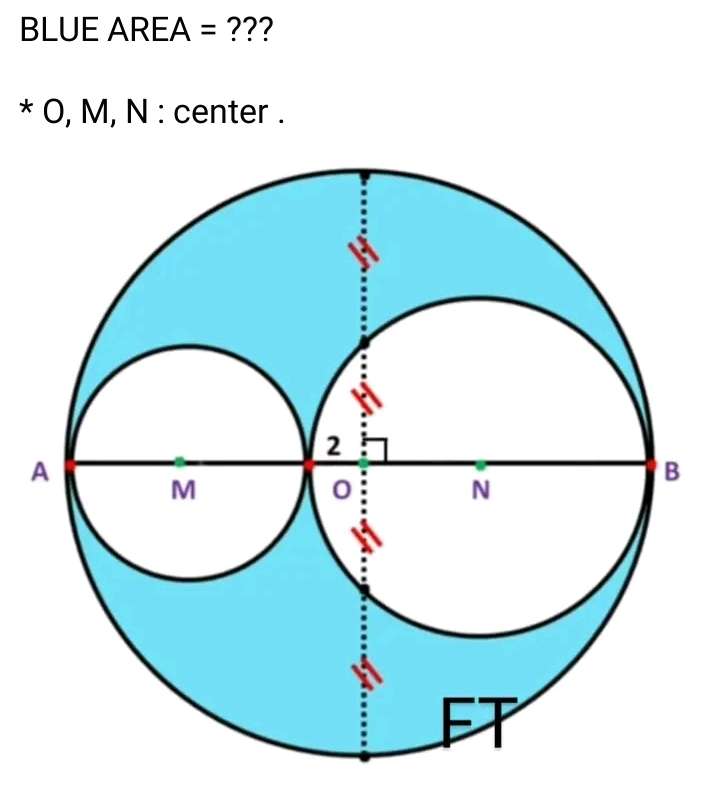
Let a be the area of the ascribed circle.
b = ½(a) units.
c = (a+2) units.
d = ½(c)
d = ½(a+2) units.
d is the radius of the big inscribed circle.
e = (a-2) units.
f = ½(e)
f = ½(a-2) units.
f...
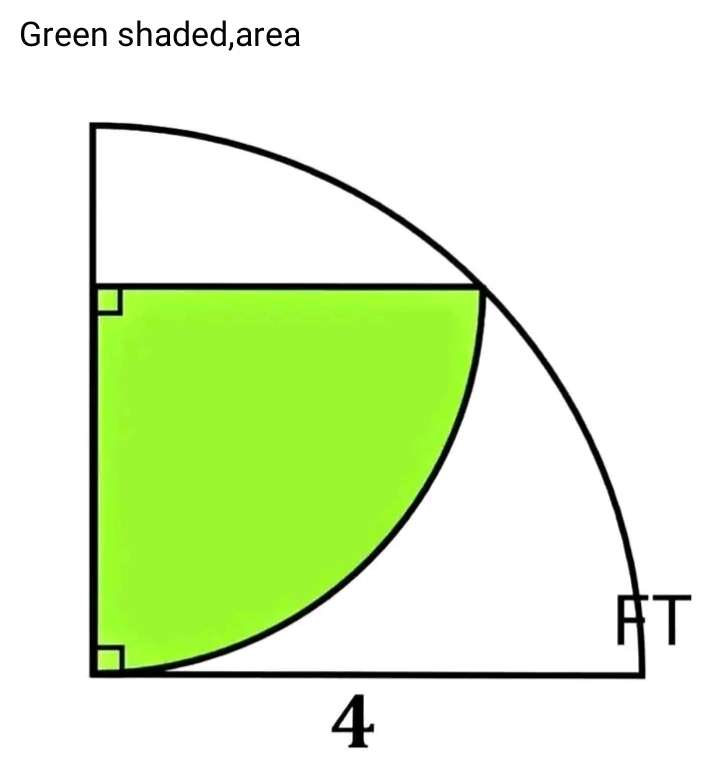
Calculating area green inscribed quarter circle.
Let it's radius be a.
It implies;
2a² = 4²
a² = 8
a = 2√(2) units.
Therefore, area green inscribed quarter circle is;
¼*π*a²
= ¼*π*2√(2)*2√(2)
=...

It implies;
Calculating x.
(½*x*3x)+(½(2x+3x)*3x) = 12
3x²+15x² = 24
18x² = 24
x² = 4/3
x = ⅓(2√(3)) units.
Therefore, 3x, the side length of the ascribed square
is;
3*⅓(2√(3))
= 2√(3) units ...
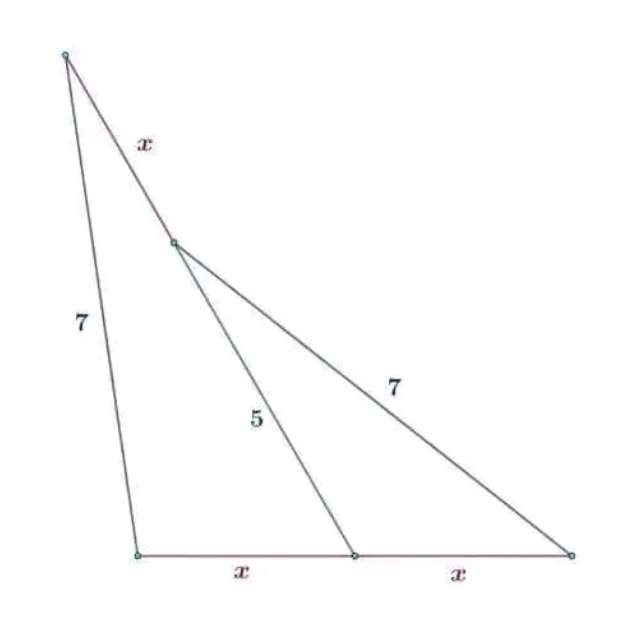
Calculating x.
7² = x²+5²+2*5*xcosa
49 = x²+25+10xcosa
24 = x²+10xcosa
10xcosa = 24-x²
cosa = (24-x²)/(10x) --- (1).
b = (x+5) units.
7² = x²+(x+5)²-2x(x+5)cosa
49 = x²+x²+10x+25-(2x²+10x)cosa
2...
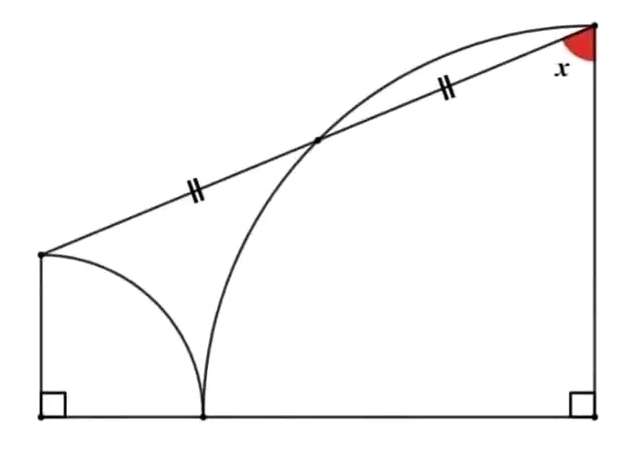
The required angle, x is;
a = ½(90)
a = 45°
it implies;
x = ½(180-a)
x = ½(180-45)
x = ½(135)
x = 67.5°