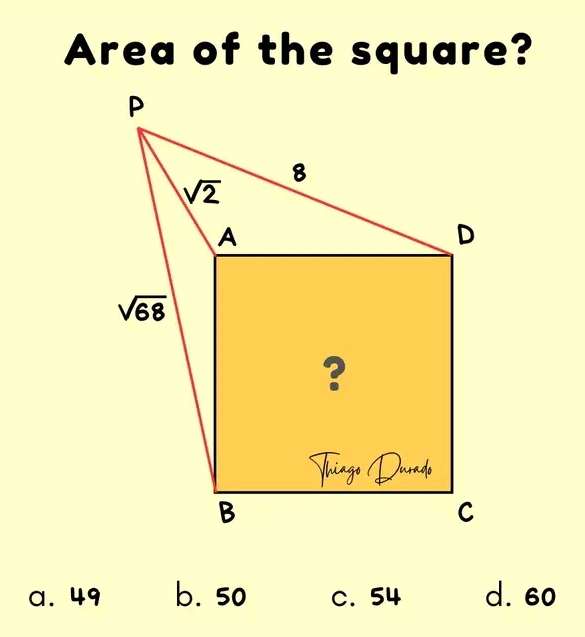
Let the square side length be a.
It implies;
Area square is a²
Calculating a² (Area of the Square).
√(2)² = b²+c²
c = √(2-b²) --- (1).
√(68)² = (a+b)²+c²
68 = (a+b)²+√(2-b²)²
68 = (...

a = 180-60
a = 120°
(7/sin120) = (3/sinb)
b = 21.7867892983°
c = 60+b
c = 81.7867892983°
d = 180-120-b
d = 60-21.7867892983
d = 38.2132107017°
(7/sin120) = (e/sin38.2132107017)
e...

Sir Mike Ambrose is the author of the question.
Area rectangle is;
9x8 = 72 square unit.
Area green is;
Area trapeziod with two parallel lengths (5+2-¾) unit and height 5 unit - Area sect...

Blue Area will be;
2(area circle of radius 1 unit - 2(2(area sector of radius 1 unit and angle 60°) - area equilateral triangle of two side length 1 unit and angle 60°))
= 2(π - 2(2(π/6) - ¼...
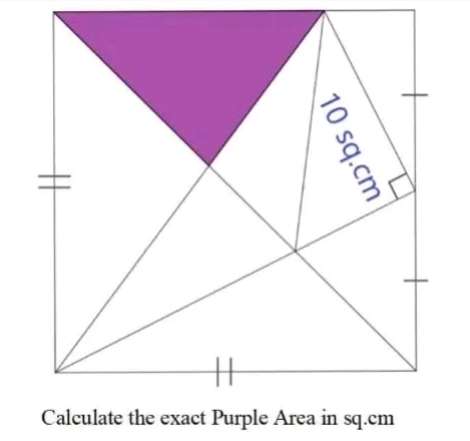
Sir Mike Ambrose is the author of the question.
Let the side length of the square be a.
tanb = a/(0.5a)
b = atan(2)°
c = 180-b-45
c = (135-atan(2))°
(0.5a/sin(135-atan(2)) = (d/sin45)...
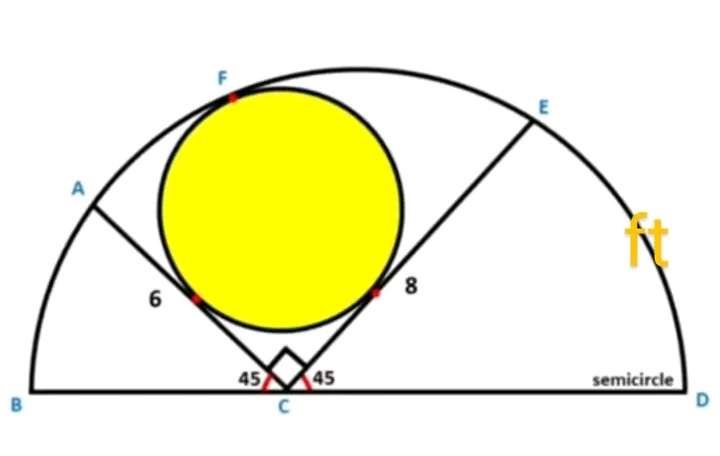
Calculating yellow inscribed circle area.
a² = 6²+8²
a = √(100)
a = 10 units.
2b² = 10²
b² = 50
b = 5√(2) units.
b is the radius of the half circle.
(5√(2)/sin45) = (8/sinc)
c = 53....
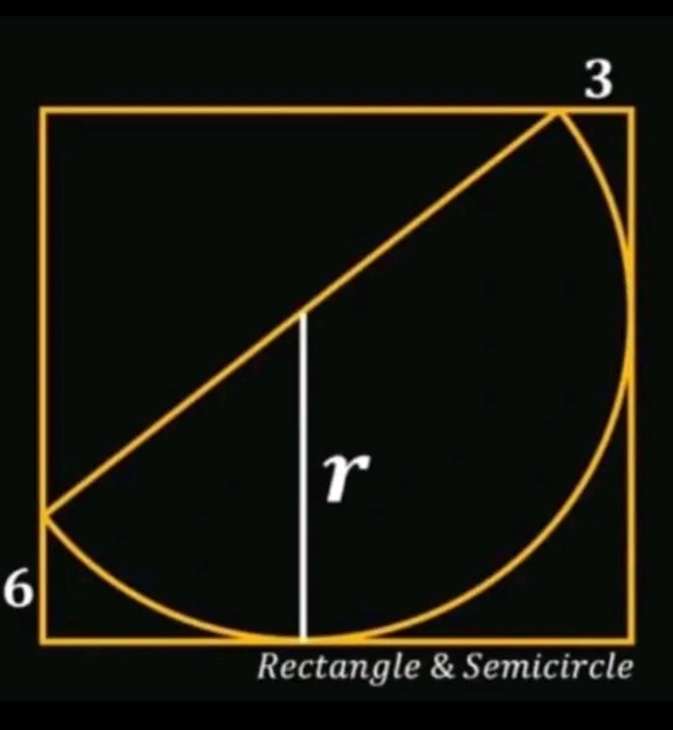
Calculating r, radius of the inscribed half circle.
a = (r-3) units.
b = (r-6) units.
It implies;
r² = a²+b²
r² = (r-3)²+(r-6)²
r² = r²-6r+9+r²-12r+36
r²-18r+45 = 0
Resolving the...
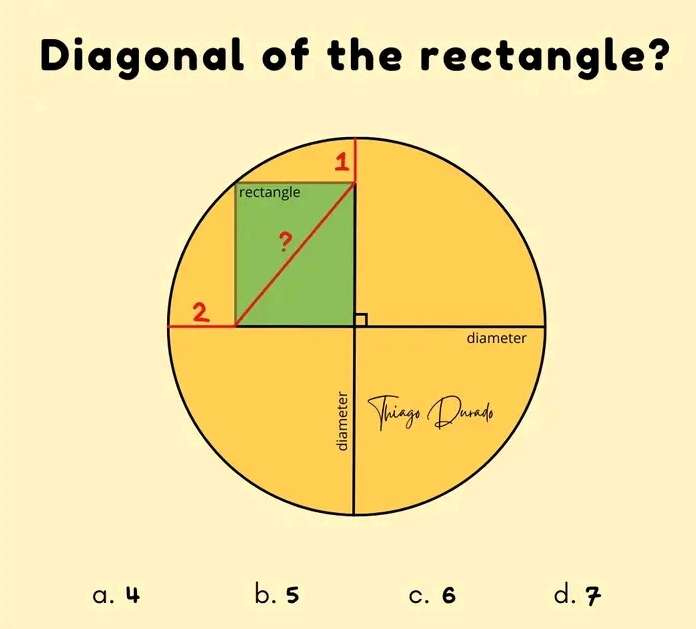
Notice!
Diagonal of the inscribed rectangle is also the radius of the ascribed circle.
Let it be a.
b = (a-2) units.
c = (a-1) units.
It implies;
a² = (a-1)²+(a-2)²
a² = a²-2a+1+...
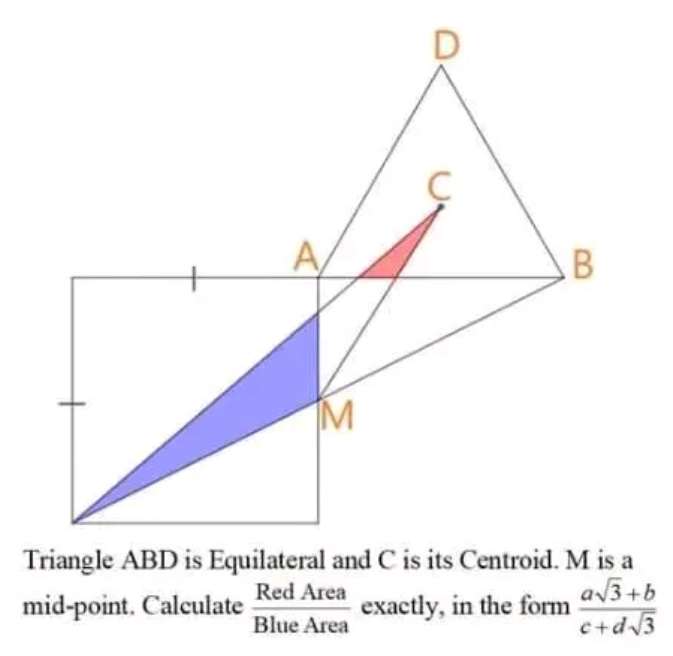
Sir Mike Ambrose is the author of the question.
Let the single side length of the square be 2 unit.
Therefore;
Area blue is;
Area triangle of height (12+2√(3))/9 unit and base 2 unit -...
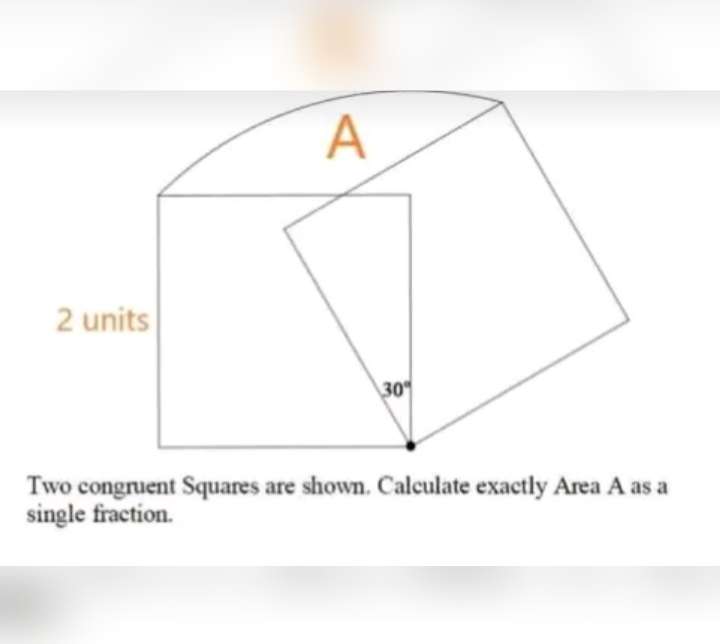
Sir Mike Ambrose is the author of the question.
Area A exactly as a single fraction is;
Area sector with radius 2√(2) units and angle 60° - Area equilateral triangle with side 2√(2) units+ Ar...