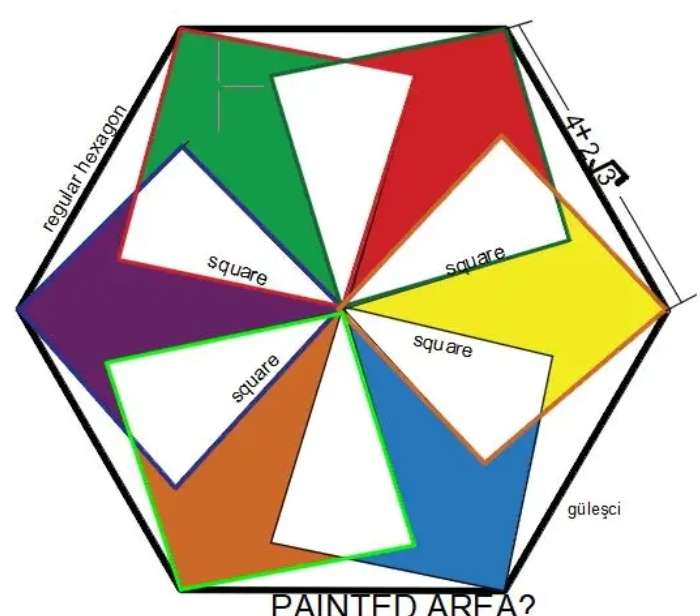
Mathematics Question and Solution
Notice!
(4+2√(3)) units = 7.4641016151 units is the side length of the regular hexagon.
a = ⅙*180(6-2)
a = ⅙(180*4)
a = 120°
a is the single interior angle of the regular hexagon.
b = ½(a)
b = ½(120)
b = 60°
c = b-45
c = 60-45
c = 15°
d = 180-2c
d = 180-2*15
d = 150°
cos15 = (0.5(4+2√(3))/e
e = 3.8637033052 units.
f = ½(d)
f = ½(150)
f = 75°
Let g be the side length of the inscribed congruent squares.
h = g-e
h = (g-3.8637033052) units.
Therefore;
tan75 = g/(g-3.8637033052)
g = gtan75-3.8637033052tan75
3.8637033052tan75 = gtan75-g
g = 3.8637033052tan75/(tan75-1)
g = 5.2779168676 units.
Again, g is the side length of the inscribed congruent squares.
h = g-e
h = 5.2779168676-3.8637033052
h = 1.4142135624 units.
Therefore, the painted areas is;
6(area square with side 5.2779168676 units - 2(area rectangle with length 5.2779168676 units and width 1.4142135624 units)).
= 6((5.2779168676)²-2(5.2779168676*1.4142135624))
= 6(27.8564064613-2*7.4641016154)
= 6(27.8564064613-14.9282032308)
= 6(12.9282032305)
= 77.5692193832 square units.