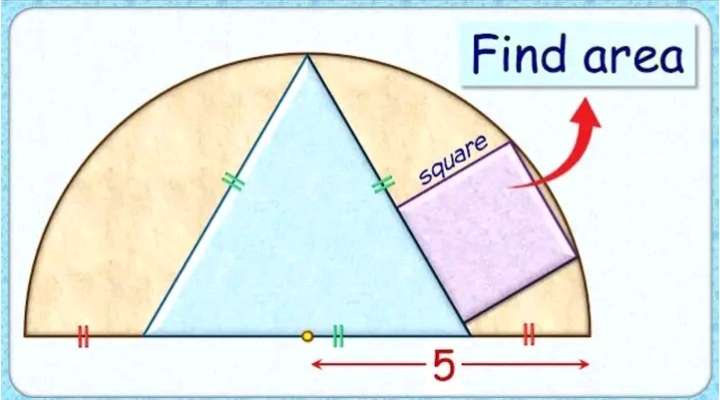
Mathematics Question and Solution
sin60 = 5/a
a = 5/(√(3)/2)
a = ⅓(10√(3)) units.
a is the side length of the inscribed regular triangle.
b = ½(a)
b = ⅓(5√(3)) units.
sin60 = c/⅓(5√(3))
√(3)/2 = 3c/(5√(3))
6c = 15
c = 2.5 units.
Let the inscribed square side length be d.
e = (2.5+d) units.
It implies;
5² = (2.5+d)²+(0.5d)²
25 = 6.25+5d+d²+0.25d²
¼(5d²)+5d-18.75 = 0
¼(d²)+d-3.75 = 0
d²+4d-15 = 0
Resolving the above quadratic equation via completing the square approach to get d, the side length of the inscribed square.
(d+2)² = 15+2²
d = -2±√(19)
It implies;
d = (√(19)-2) units.
Again, d is the side length of the inscribed square.
Therefore, area square is;
d²
= (√(19)-2)²
= 19-4√(19)+4
= (23-4√(19)) square units.
= 5.5644042258 square units.