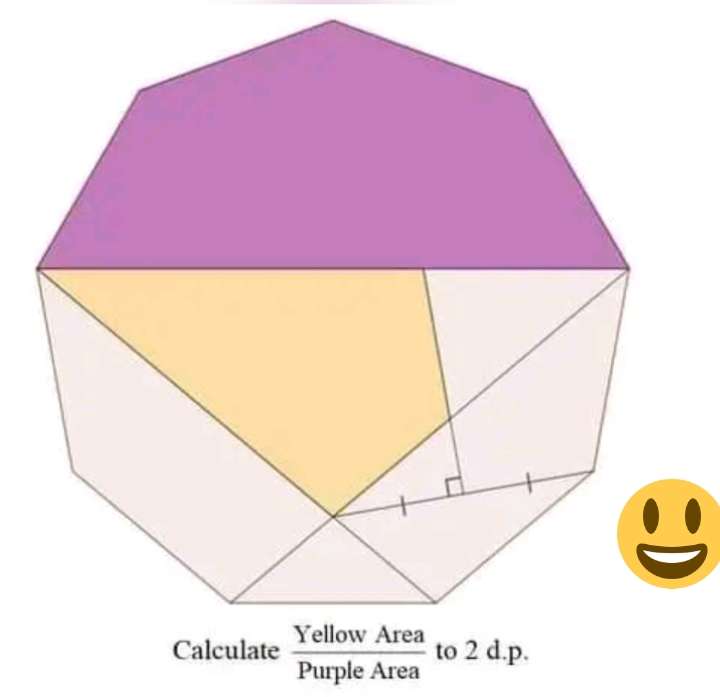
Sir Mike Ambrose is the author of the question.
Let the single side length of the regular nonagon be 2 units.
Therefore;
Area purple is;
Area triangle with two equal length 2 units each a...
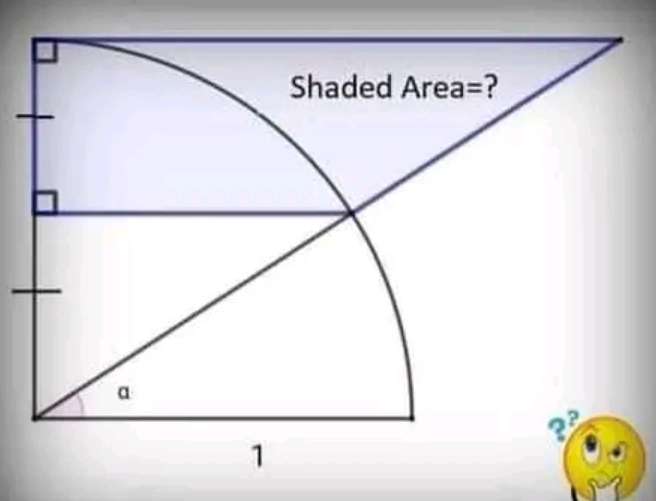
½ - 1
½√(3) - x.
Where x is the base of the blue shaded trapezium.
Cross multiply
½(x) = ½(√(3))
Therefore x = √(3) units.
Therefore area blue (area trapezium) is;
½*½(½√(3)+√(3))...
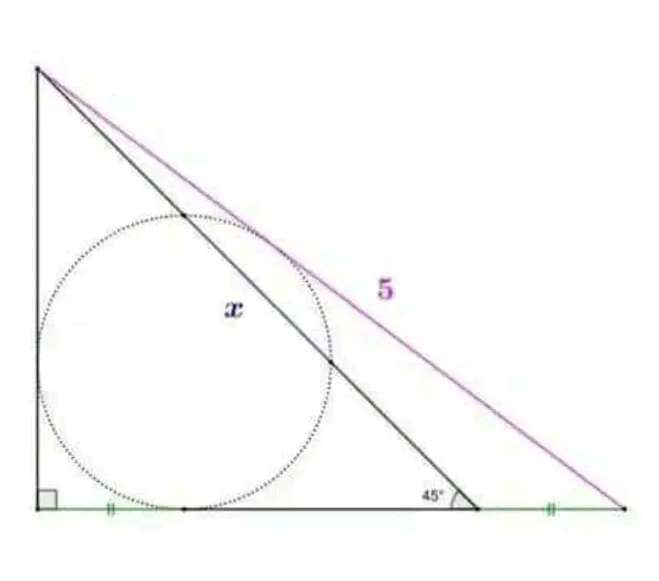
Let a be the radius of the inscribed circle.
Calculating a.
b = 3a units.
c = b+a
c = 4a units.
It implies;
3a²+4a²+5a = 3a*4a
7a²+5a = 12a²
5a² = 5a
a = 1 unit.
Again, a is the...
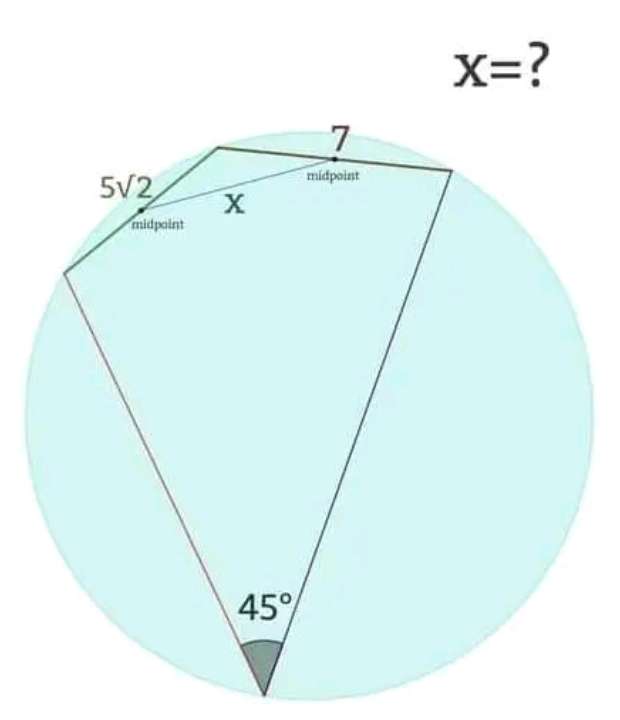
X will be;
√((½*5√(2))²+(½*7)²-(½*5√(2)*½*7*2cos135)
= √(½*25+¼*49-½*35√(2)cos135)
= √((50+49-70√(2)cos135)/4)
= ½√(99-70√(2)cos135)
= ½√(169)
= ½(13)
= 6.5 unit
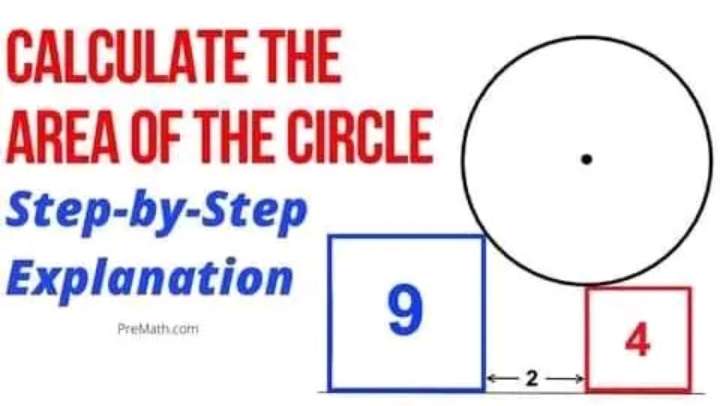
Area circle is;
Let the radius of the circle be r.
r²=2²+(r-1)²
r²=4+r²-2r+1
r = 2.5 units.
Therefore;
Area circle is;
π(2.5)²
= 6.25π square units.
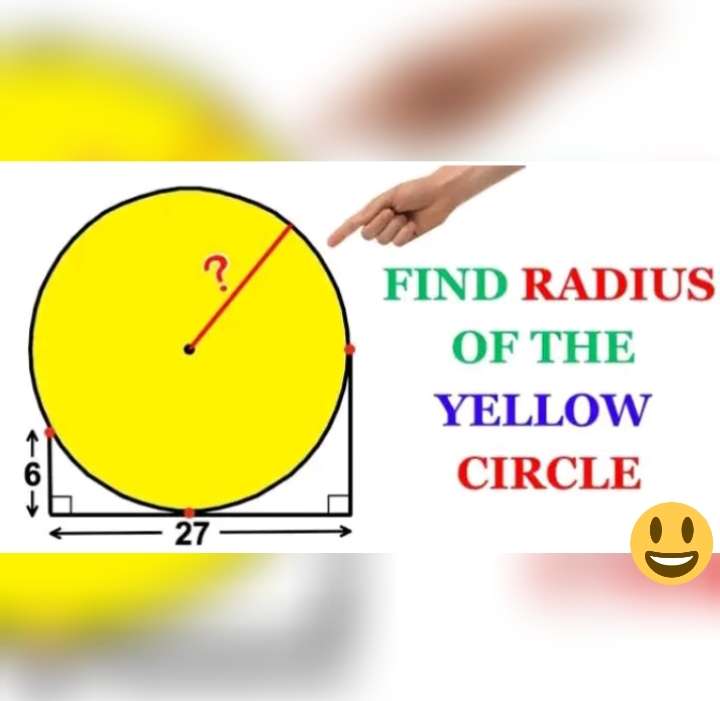
Calculating the radius of the circle.
Let a be the radius of the circle.
b = (27-a) units.
c = (a-6) units.
Therefore;
a² = (a-6)²+(27-a)²
a² = a²-12a+36+729-54a+a²
a²-66a+765 = 0...
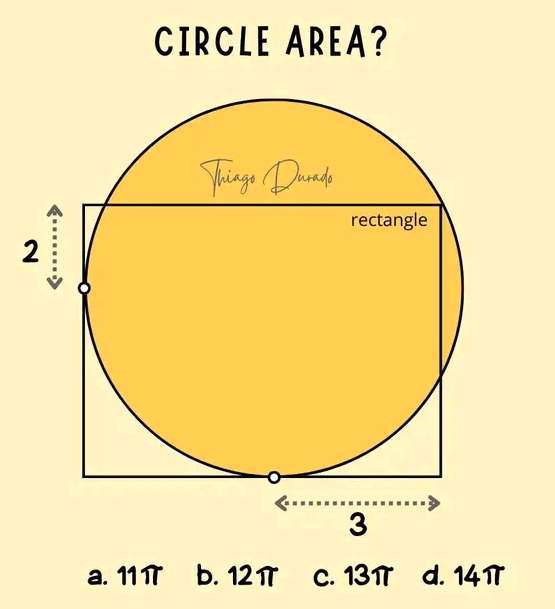
Let a be the radius of the circle.
Therefore;
a² = 2²+3²
a = √(13) units.
Again, a is the radius of the circle.
Are circle is;
πa²
= π√(13)²
= 13π square units.
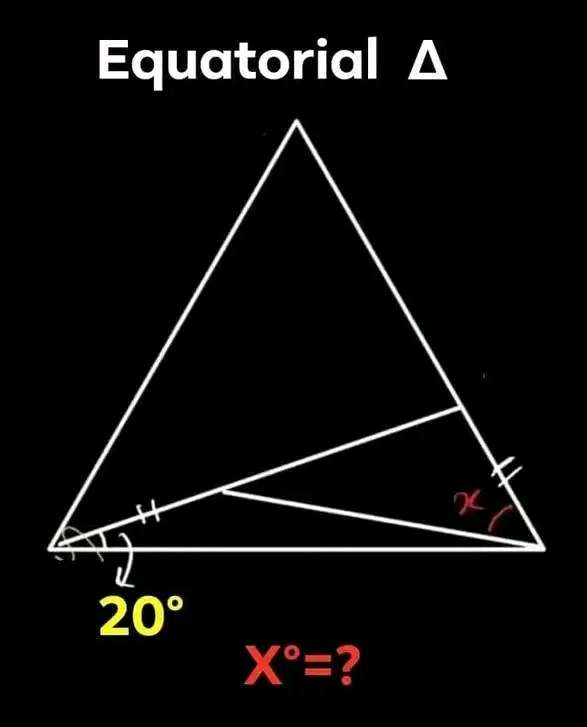
Notice!
The ascribed triangle is equilateral.
Let the two equal lengths of the composite plane shape be 1 unit each.
a = 180-20-60
a = 100°
(1/sin100) = (b/sin20)
b = 0.3472963553 units....
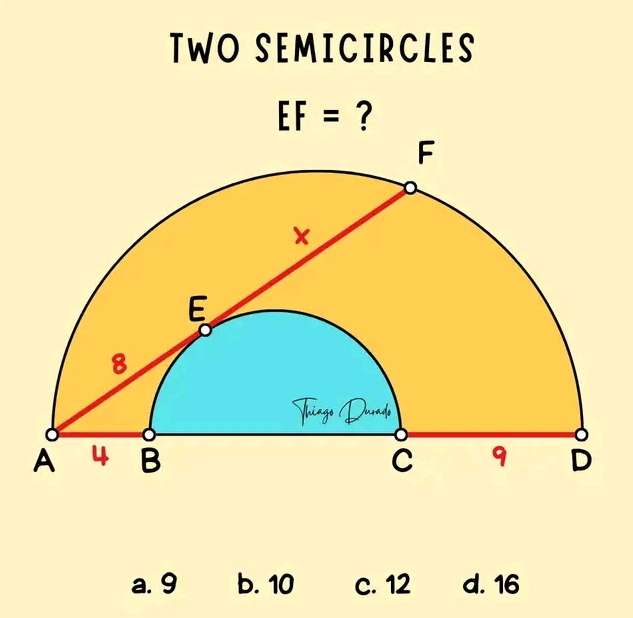
Let the blue inscribed half circle's radius be a.
It implies;
Calculating a.
(4+a)² = a²+8²
16+8a+a² = a²+64
8a = 48
a = 6 units.
Again, a is the radius of the blue inscribed half circ...
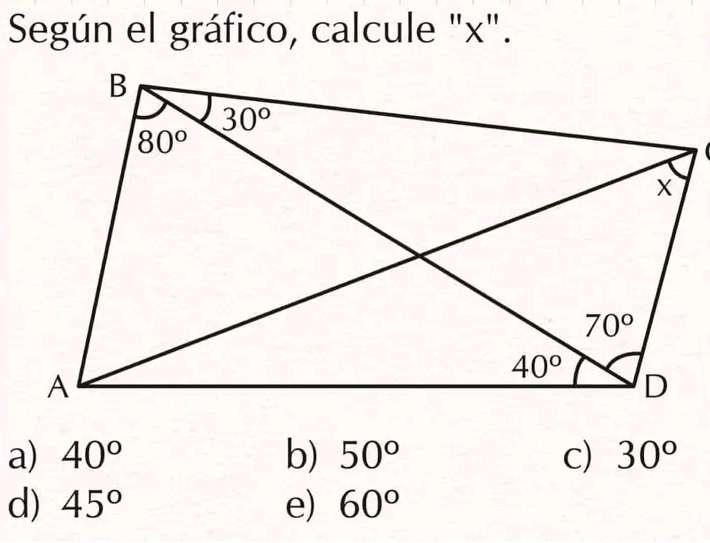
Let AB = 1 unit.
a = 180-80-40
a = 60°
a is angle BAD.
(1/sin80) = (b/sin60)
b = 0.8793852416 units.
b is BD.
c = 180-30-70
c = 80°
c is angle BCD.
(0.8793852416/sin80) = (d/sin30...