Sir Mike Ambrose is the author of the question.
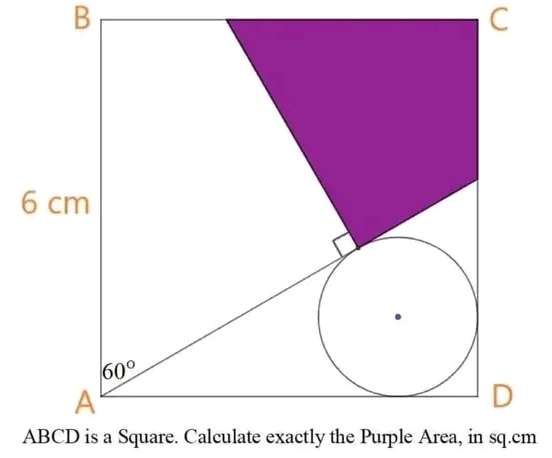
tan30 = a/6
a = 2√(3) cm.
b = (6-2√(3)) cm.
sin30 = 2√(3)/c
c = 4√(3) cm.
6d+2√(3)d+ 4√(3)d = 6*2√(3)
(6+6√(3))d = 12√(3)
d = (72√(3)-216...
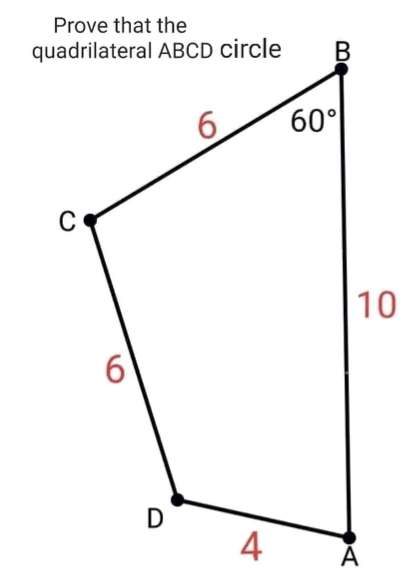
Showing that quadrilateral ABCD is cyclic.
Notice!
For quadrilateral ABCD to be cyclic;
Angle ADC will equal 2 times angle ABC.
Angle ADC = 2(Angle ABC)
It implies;
Since Angle ABC...
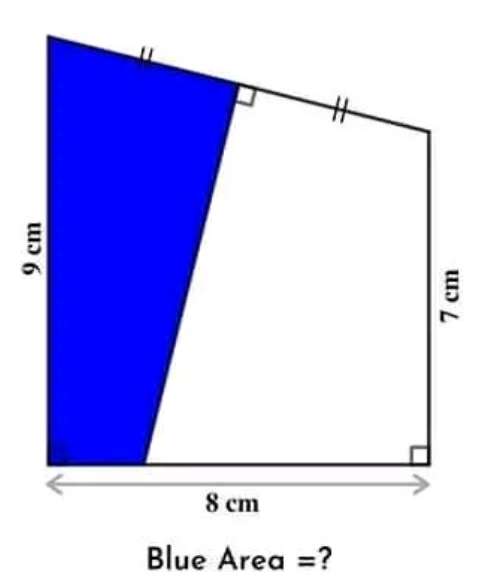
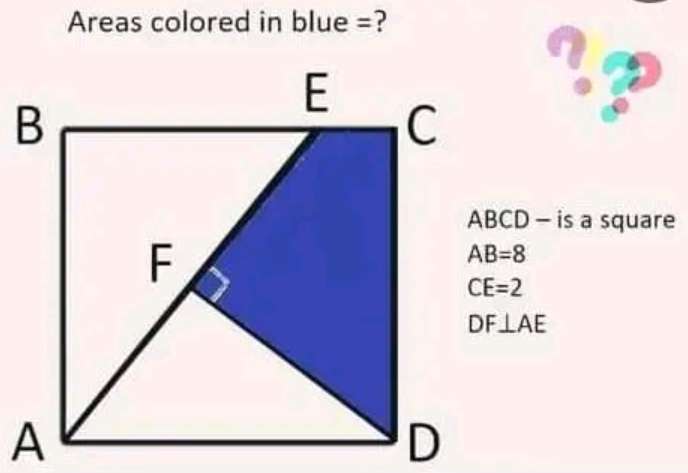
Blue area is;
½(9x2)+½(√(68)x√(17))
= 9+½(34)
= 9+17
= 26 cm²
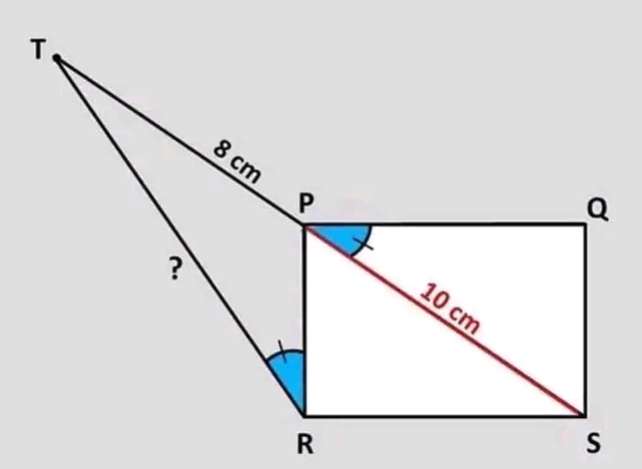
RT = √((8+5)²-5²)
RT = √(169-25)
RT = √(144)
RT = 12 cm.
RT is the required length.
Blue area will be;
½(5.2x6.4)+½(2x8)
= ½(33.28)+8
= 16.64+8.00
= 26.64 square unit.
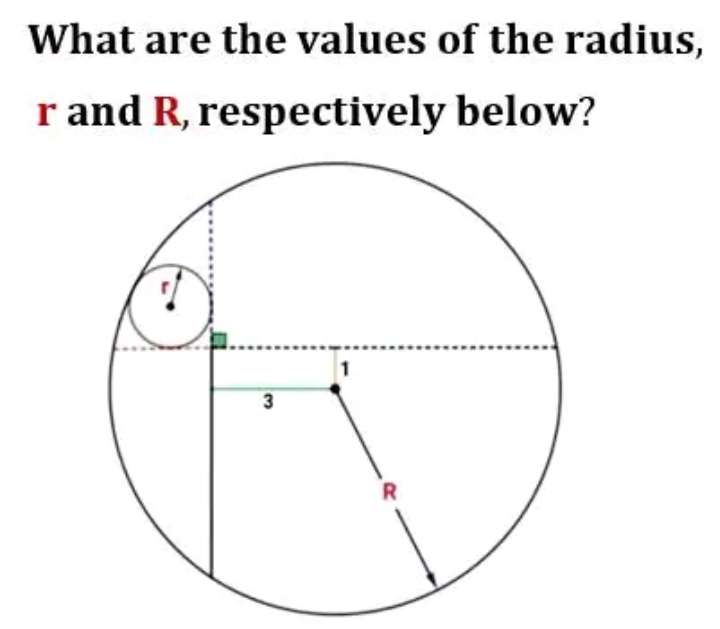
Calculating R.
a²+3² = R²
a = √(R²-9) units.
b = 1+a
b = (1+√(R²-9)) units.
c = a-1
c = (√(R²-9)-1) units.
d²+1² = R²
d = √(R²-1) units.
e = 3+d
e = (3+√(R²-1)) units.
f = d-...
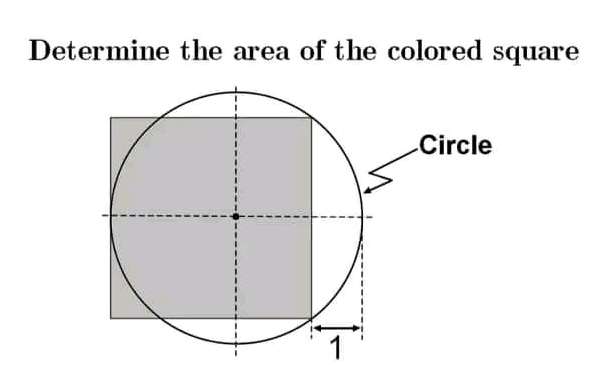
Let r be the radius of the circle.
a = (r-1) units.
b = (r-0.5) units.
Calculating r.
It implies;
r² = (r-1)²+(r-0.5)²
r² = r²-2r+1+r²-r+(¼)
0 = r²-3r+(5/4)
4r²-12r+5 = 0
4r²-2r-...
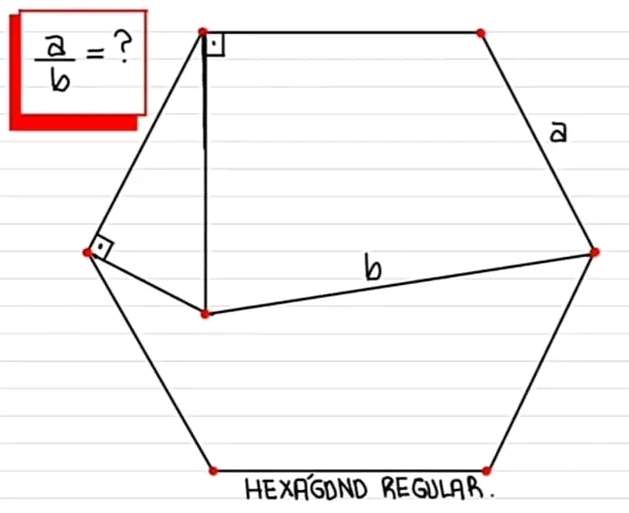
Let a be 1 units.
a is the side length of the regular hexagon.
Calculating b.
c = 120-90
c = 30°
120° is the single interior angle of the regular hexagon.
cos30 = 1/d
d = 2/√(3)
d = ⅓(2√(3)) unit...
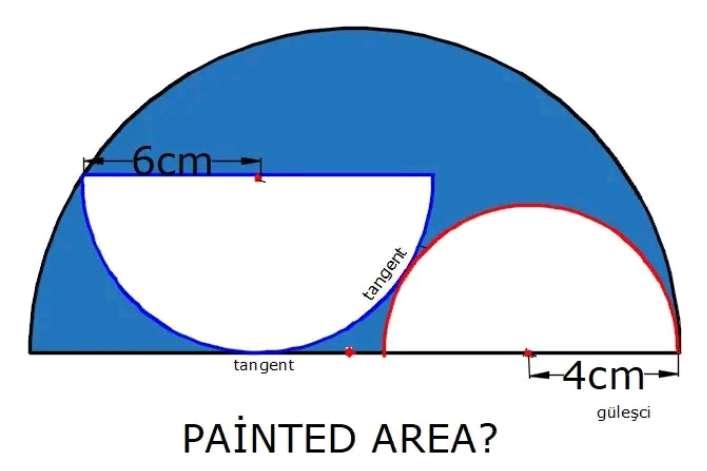
a = 6+4
a = 10 cm.
b²+6² = 10²
b = √(100-36)
b = √(64)
b = 8 cm.
c = b+4
c = 12 cm.
d = c-r
d = (12-r) cm.
r is the ascribed half circle radius.
e = 6+d
e = 6+(12-r)
e = (18-r)...
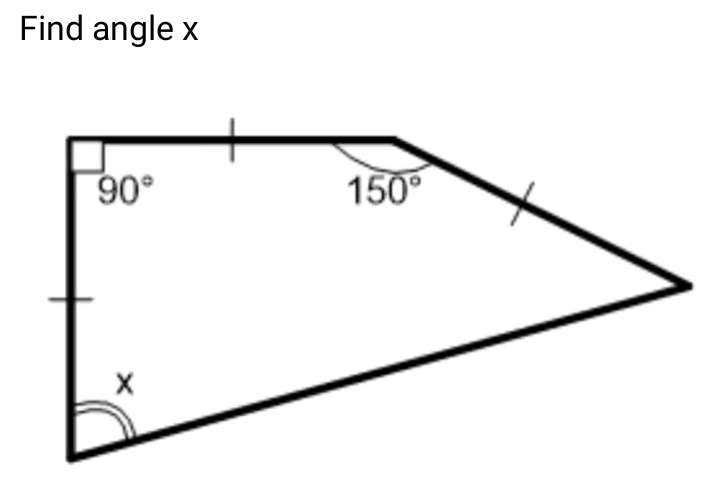
Let the three equal lengths be 1 unit each.
a² = 1²+1²
a = √(2) units.
b = 150-45
b = 105°
c² = √(2)²+1²+2√(2)cos 105
c = 1.9318516526 units.
(1.9318516526/sin105) = (1/sind)
d = 30...