
Sir Mike Ambrose is the author of the question.
Area rectangle is;
9x8 = 72 square unit.
Area green is;
Area trapeziod with two parallel lengths (5+2-¾) unit and height 5 unit - Area sect...

Blue Area will be;
2(area circle of radius 1 unit - 2(2(area sector of radius 1 unit and angle 60°) - area equilateral triangle of two side length 1 unit and angle 60°))
= 2(π - 2(2(π/6) - ¼...
Sir Mike Ambrose is the author of the question.
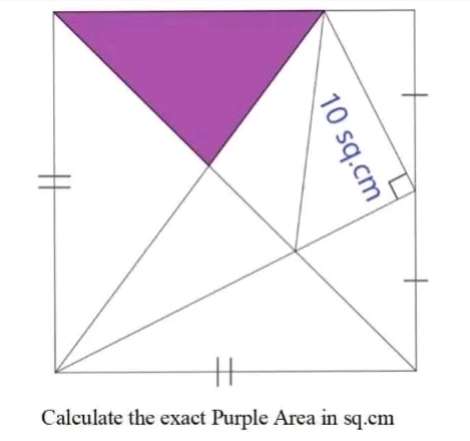
Let the side length of the square be a.
tanb = a/(0.5a)
b = atan(2)°
c = 180-b-45
c = (135-atan(2))°
(0.5a/sin(135-atan(2)) = (d/sin45)...
Calculating yellow inscribed circle area.
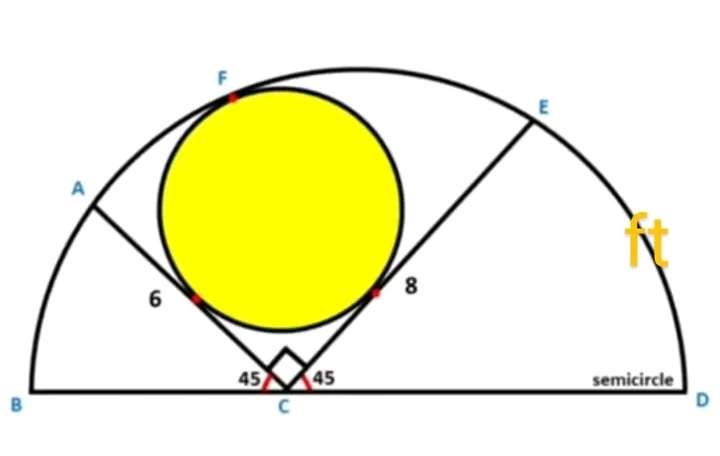
a² = 6²+8²
a = √(100)
a = 10 units.
2b² = 10²
b² = 50
b = 5√(2) units.
b is the radius of the half circle.
(5√(2)/sin45) = (8/sinc)
c = 53....
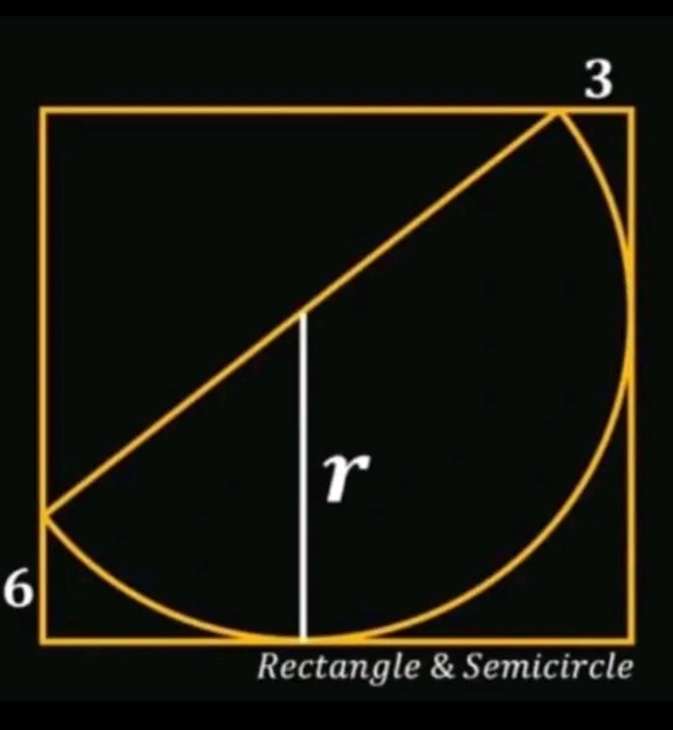
Calculating r, radius of the inscribed half circle.
a = (r-3) units.
b = (r-6) units.
It implies;
r² = a²+b²
r² = (r-3)²+(r-6)²
r² = r²-6r+9+r²-12r+36
r²-18r+45 = 0
Resolving the...
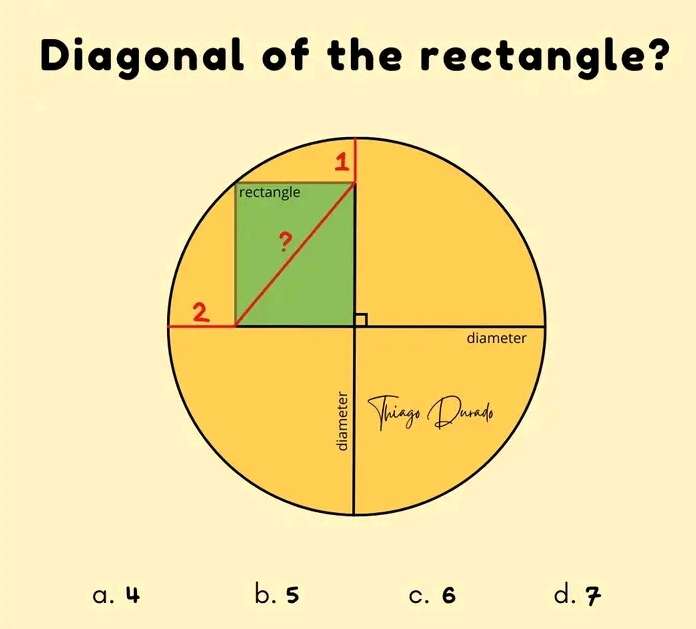
Notice!
Diagonal of the inscribed rectangle is also the radius of the ascribed circle.
Let it be a.
b = (a-2) units.
c = (a-1) units.
It implies;
a² = (a-1)²+(a-2)²
a² = a²-2a+1+...
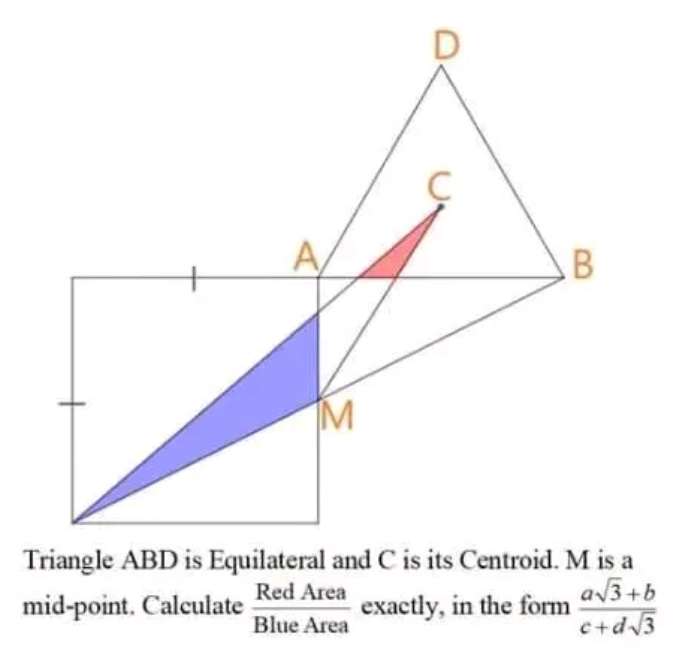
Sir Mike Ambrose is the author of the question.
Let the single side length of the square be 2 unit.
Therefore;
Area blue is;
Area triangle of height (12+2√(3))/9 unit and base 2 unit -...
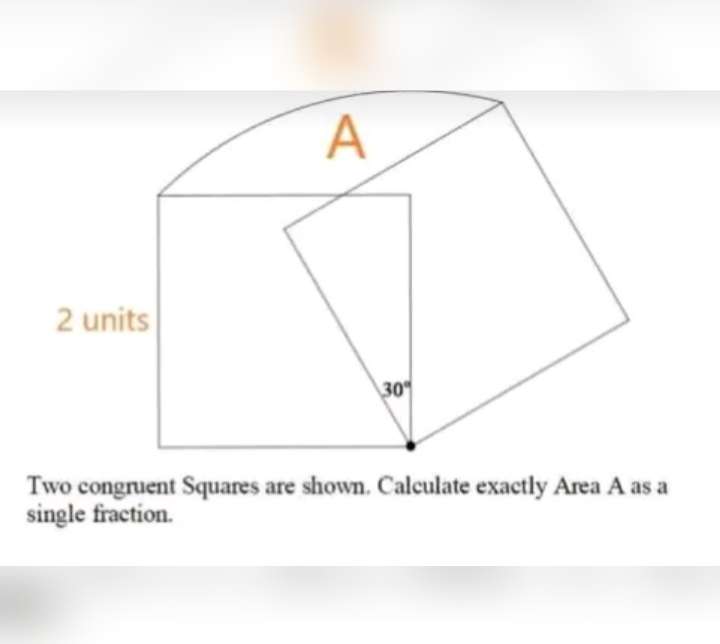
Sir Mike Ambrose is the author of the question.
Area A exactly as a single fraction is;
Area sector with radius 2√(2) units and angle 60° - Area equilateral triangle with side 2√(2) units+ Ar...
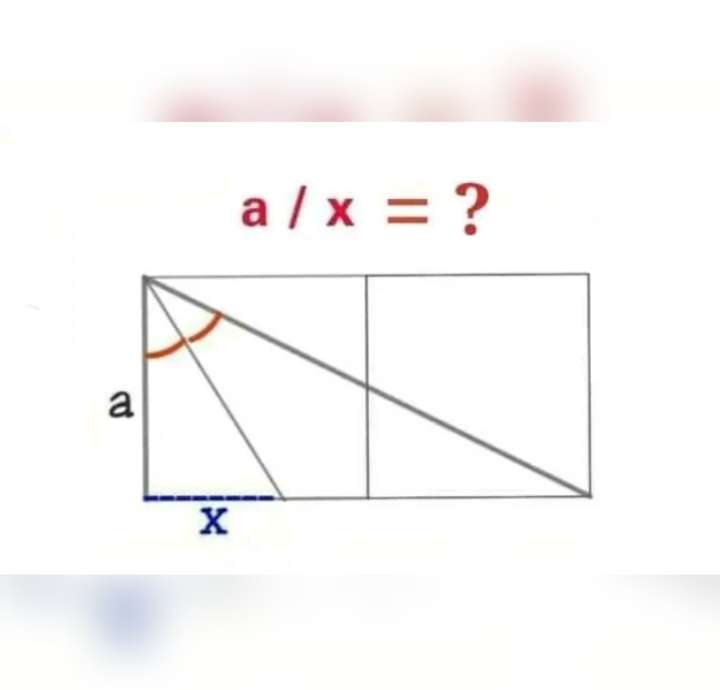
Let a, the side length of the two equal squares be 1 unit.
tanb = 1/2
b = atan(½)°
c = 90-b
c = (90-atan(½))°
c = atan(2)°
d = ½(atan2)°
It implies;
tan(0.5atan(2)) = x/1
0.61803...
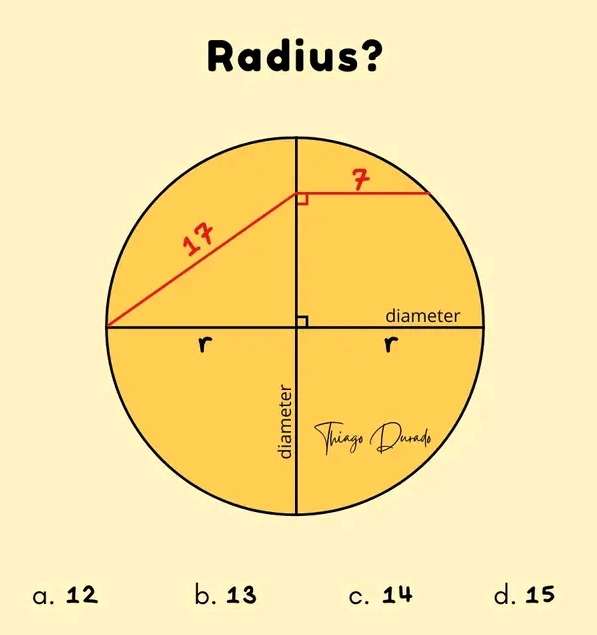
Calculating r, radius of the circle.
a²+r² = 17²
a = √(289-r²) units.
It implies;
r² = √(289-r²)²+7²
2r² = 289+49
2r² = 338
r² = 169
r = 13 units.