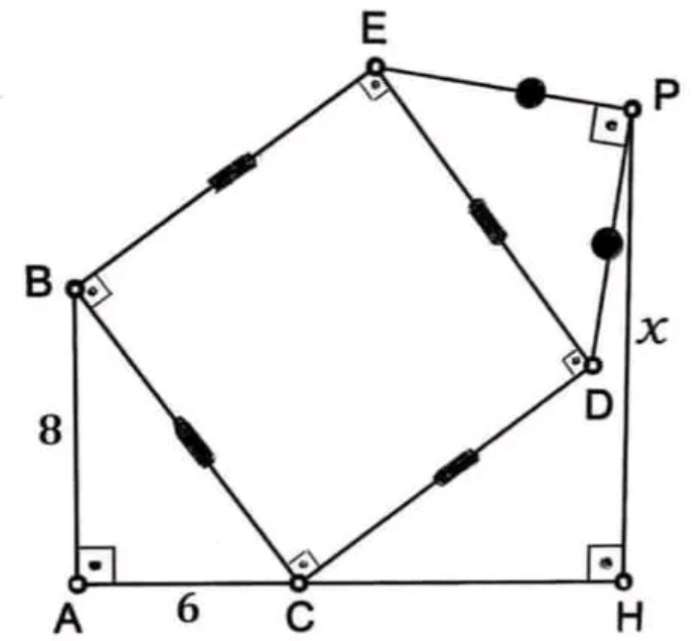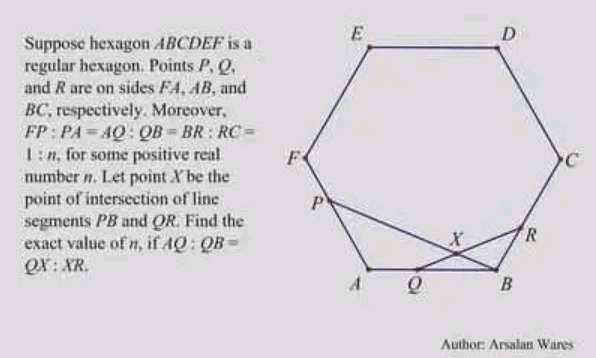
Considering similar triangle (scalene) side length ratios.
n - 1
n+1 - n
Cross multiply.
Therefore;
n²=n+1
n²-n-1=0
(n-½)²=1+¼
n =½±½(√(5))
Therefore;
n ≠ ½(1-√(5))
n = ½(...
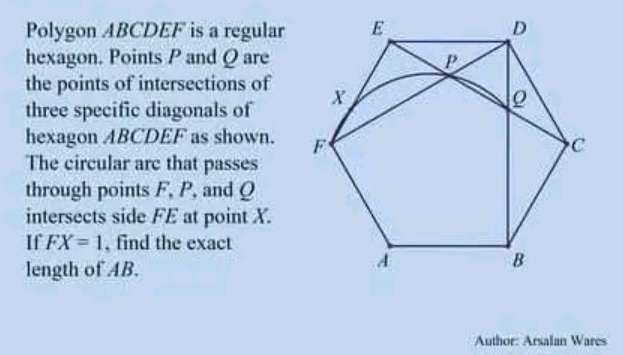
Let length AB be x.
A careful analysis carried out on the given composite plane shape lead to the derivation of right-angled tiangle EQX with hypotenuse QX ⅓(4x) and the two adjacent side of the...
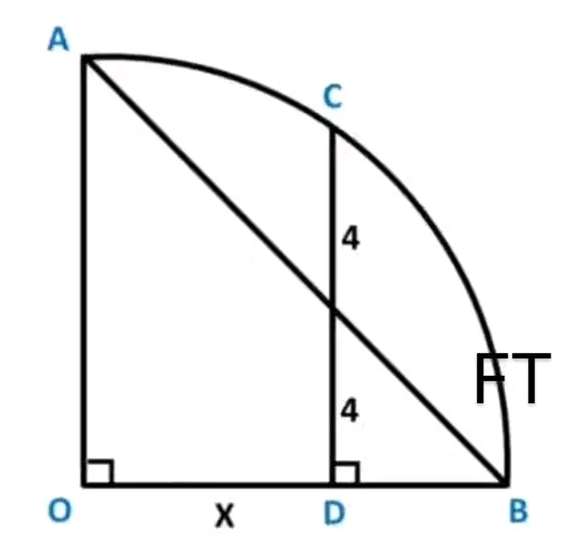
Calculating x (length OD).
a = (x+4) units.
a is the radius of the quarter circle (length OA = length OB).
It implies;
(x+4)² = 8²+x²
x²+8x+16 = 64+x²
8x = 48
x = 6 units.
Again, x is...
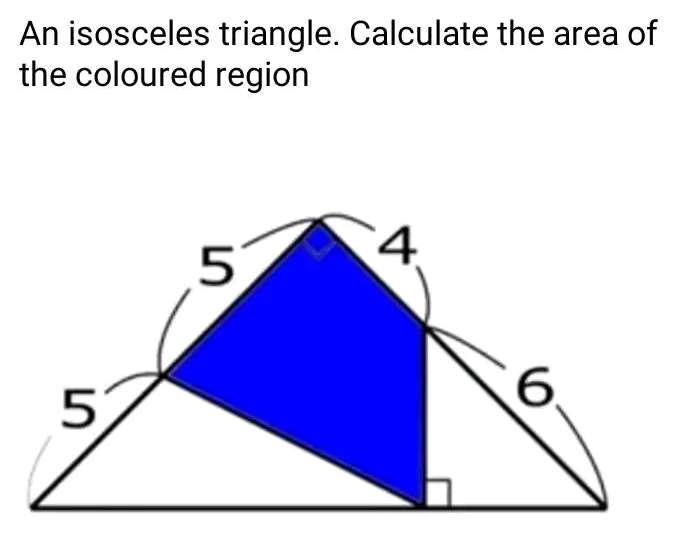
Area Coloured Region is;
Area triangle with height and base 10 units - Area triangle with height and base 3√(2) units - Area triangle with height 5 units and base 7√(2)sin45 units
= ½*10*10)...
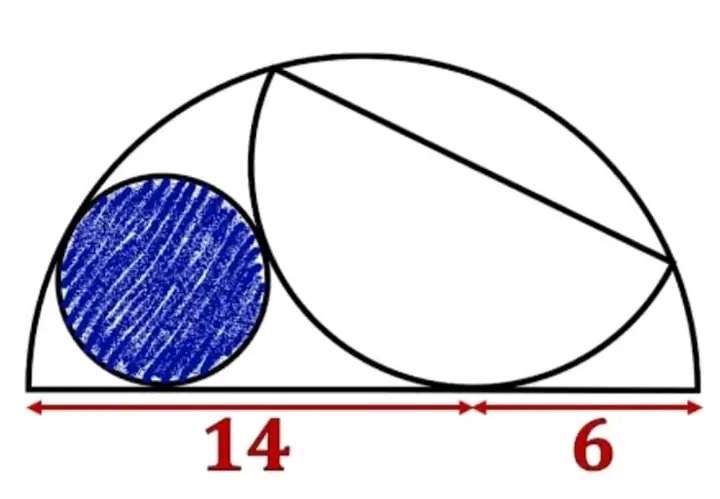
Calculating the area of the inscribed blue circle.
a = ½(14+6)
a = 10 units.
a is the radius of the ascribed semi circle.
b = a-6
b = 4 units.
c²+4² = d²
c is the radius of the inscrib...
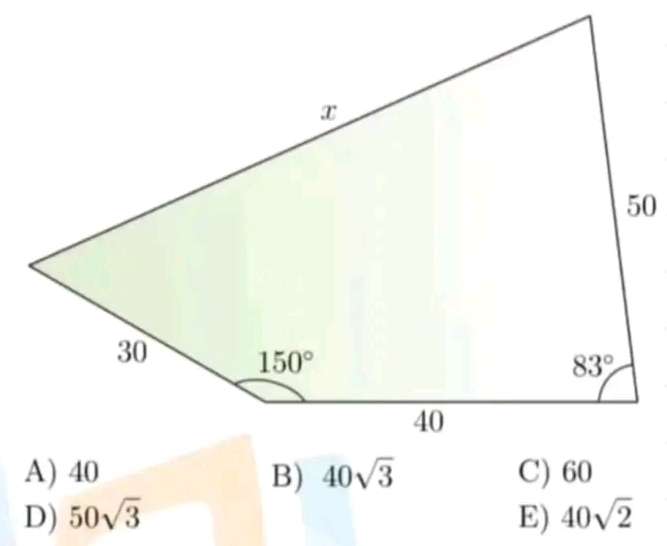
a² = 30²+40²-2*30*40cos150
a = 67.6643256752 units.
(67.6643256752/sin(150)) = (30/sinb)
b = 12.807876266°
c = 83-b
c = 70.192123734°
It implies, the required length x is;
x² = 50²+6...
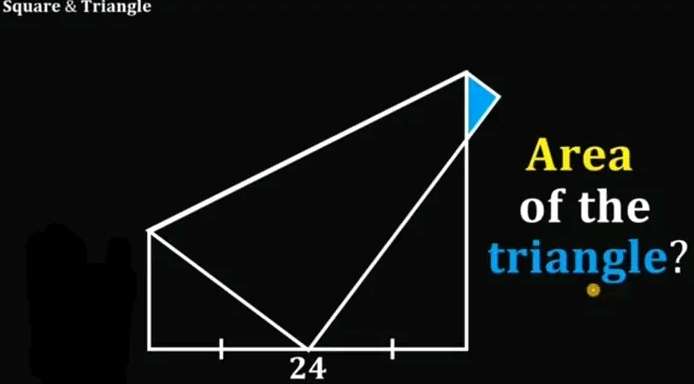
c²+12² = b²
c = √(b²-144) units.
For b = 15 units.
c = √(15²-144
c = 9 units.
tana = 12/9
a = atan(4/3)°
cos(atan(4/3)) = 12/d
⅗ = 12/d
d = 20 units.
e = 24-d
e = 4 units.
It im...
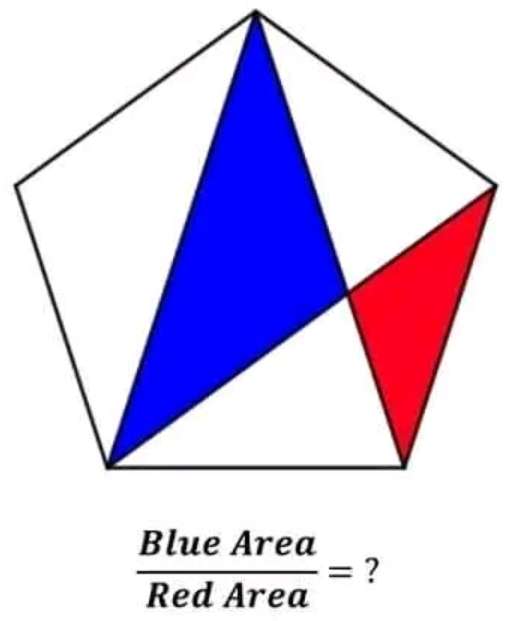
Let the single side length of the regular pentagon be 1 unit.
Therefore;
Area blue is;
½(sin108) square unit.
Area red is;
(1-cos36)sin108 square unit.
Therefore;
Area blue : Area...
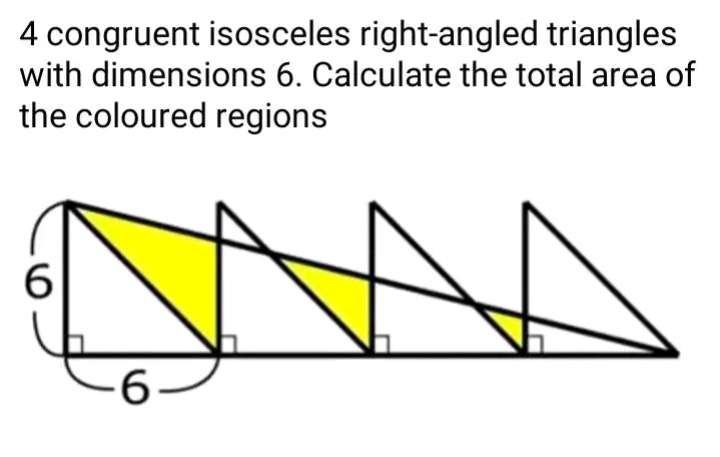
Coloured region is;
Area triangle with height 6√(2) units and base 4.5sin45 units + Area triangle with height 3 units and base 5.65685424949sin45 units + Area triangle with height 1.5 units and...