
Let the side length of the regular pentagon be 1 unit.
a² = 2-2cos108
a = 1.6180339887 units.
cos18 = b/1
b = 0.9510565163 units.
Area ascribed regular pentagon is;
½*sin108+½(1+1.618...

Calculating angle x.
a = ⅕*180(5-2)
a = 108°
a is the single interior angle of the regular pentagon.
b = 108-½(180-108)
b = 108-36
b = 72°
c = 90-72
c = 18°
d = 60+108
d = 168°...
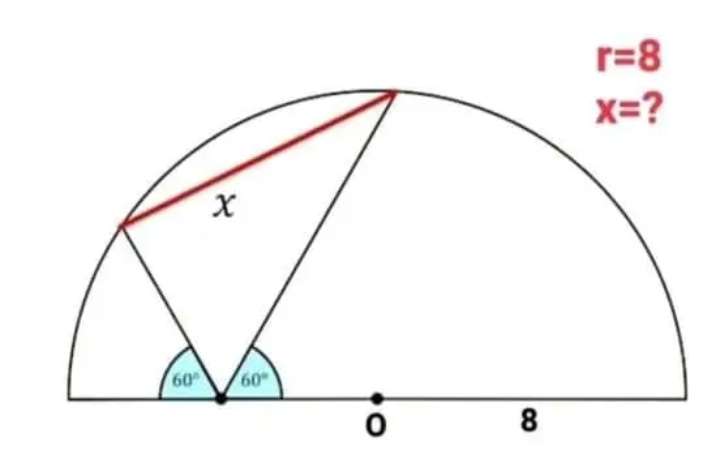
x² = 8²+8²-2*8*8cos60
x² = 128-64
x² = 64
x = √(64)
x = 8 units.
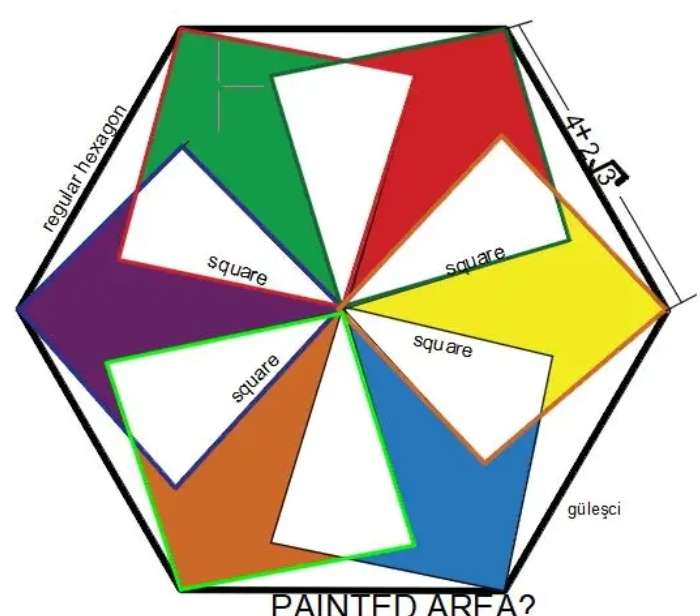
Notice!
(4+2√(3)) units = 7.4641016151 units is the side length of the regular hexagon.
a = ⅙*180(6-2)
a = ⅙(180*4)
a = 120°
a is the single interior angle of the regular hexagon.
b = ½...
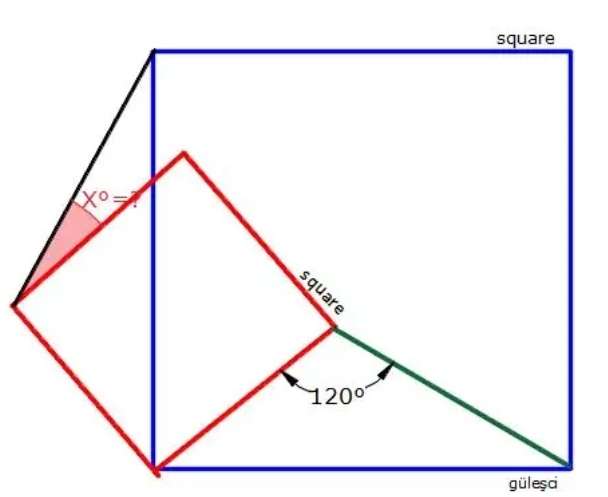
Notice!
x+90 = 120
x = 120-90
x = 30°
Where x is the required angle.
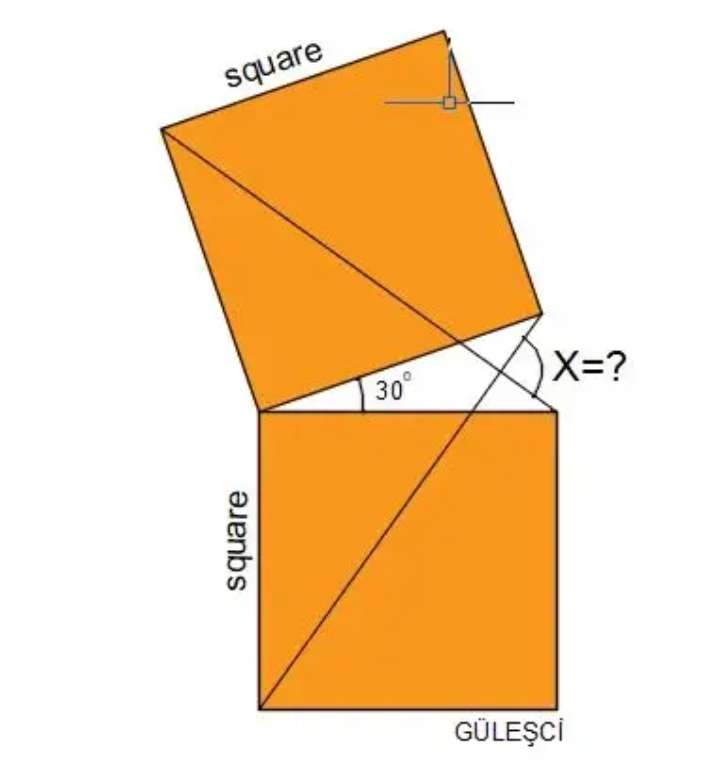
a = ½(180-90-30)
a = ½(60)
a = 30°
b = ½(180-30)
b = ½(150)
b = 75°
c = b-a
c = 75-30
c = 45°
Therefore, the required angle, x is;
x = 180-45-45
x = 180-90
x = 90°
Or
x =...
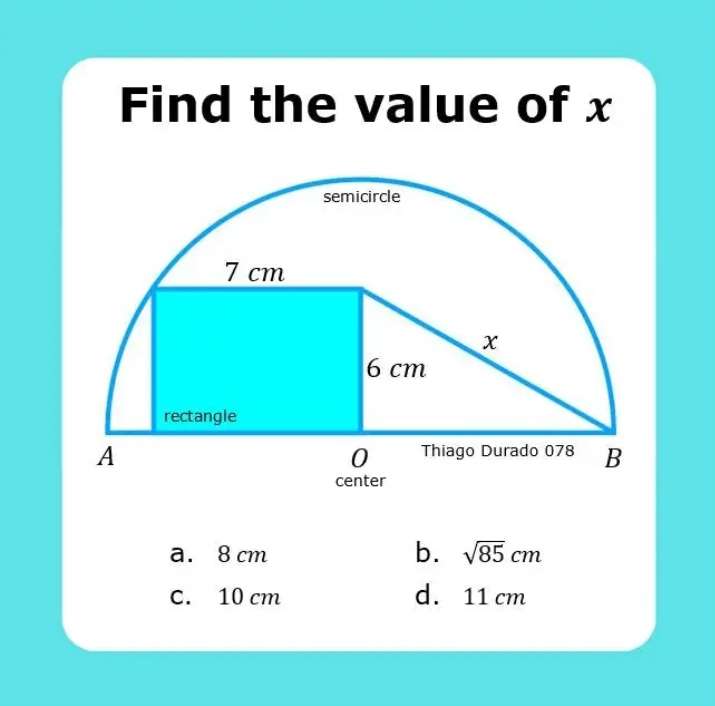
r = √(7²+6²)
r = √(85) cm.
r is the radius of the semi circle.
x² = √(85)²+6²
x² = 85+36
x = √(121)
x = 11 cm.
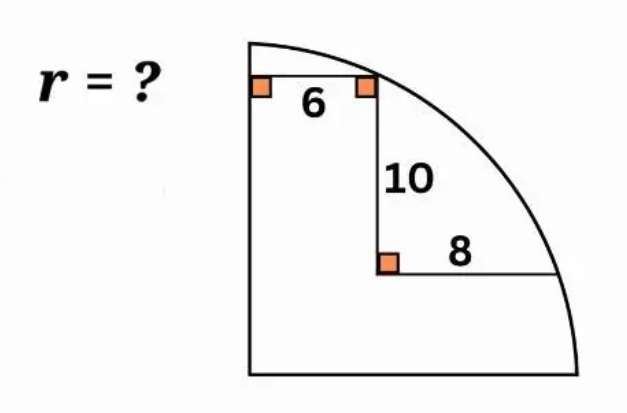
r² = x²+(6+8)² --- (1).
r² = (10+x)²+6² --- (2).
Where r is the radius of the ascribed quarter circle.
Equating (1) and (2) to get x.
r² = r²
x²+(6+8)² = (10+x)²+6²
x²+196 = 100+20x+x²+36
196-136...
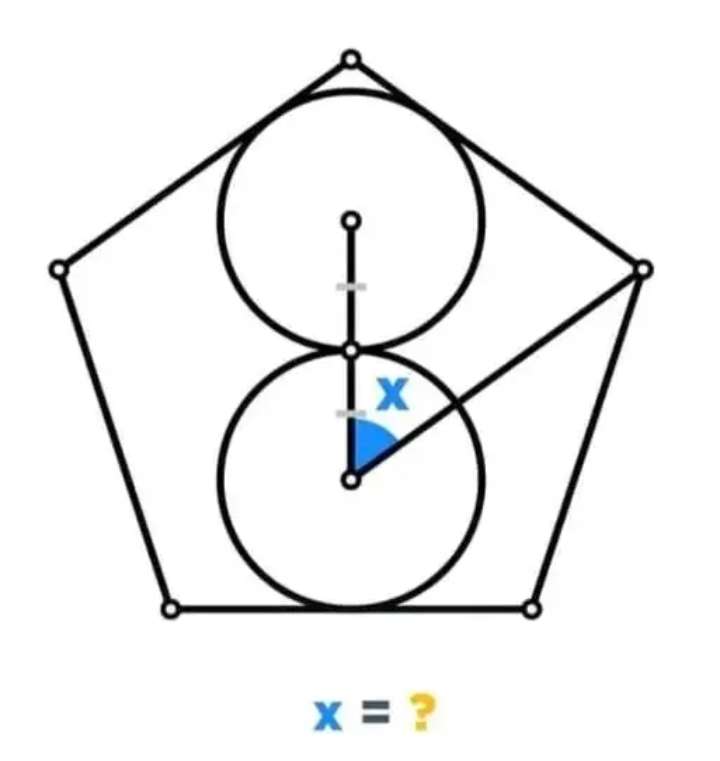
Calculating angle x.
Let the side length of the regular pentagon be 1 unit.
Calculating r, radius of the inscribed two equal circles.
a = ⅕*180(5-2)
a = 108°
b = ½(a)
b = ½*108
b = 54...