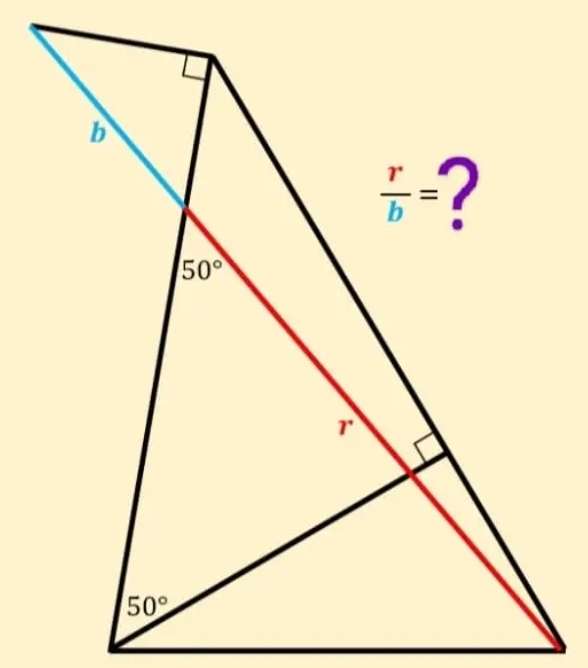
Let b = 2 units.
sin50 = c/2
c = 1.5320888862 units.
cos50 = d/2
d = 1.2855752194 units.
e = 180-50
e = 130°
f = 180-130-40
f = 10°
Calculating r.
(1.2855752194/sin10) = (r/si...
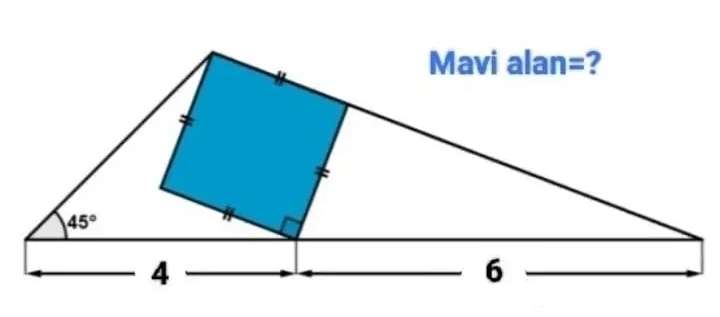
Let the side length of the inscribed blue square be a.
b²+a² = 6²
b = √(36-a²) units.
c = a+b
c = (a+√(36-a²)) units.
It implies;
(a+√(36-a²)) - 6
10 - (a+√(36-a²))
Cross Multiply...
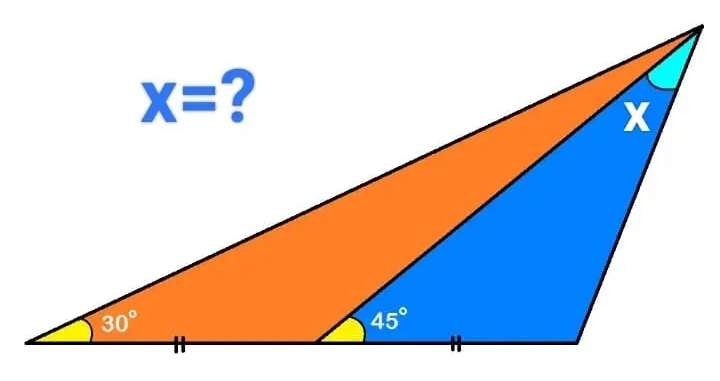
Let the base of the triangle be 2 units.
a = 180-30-135
a = 15°
(1/sin15) = (b/sin135)
b = 2.7320508076 units.
c² = 2²+2.7320508076²-2*2*2.7320508076cos30
c = 1.4142135624 units.
There...
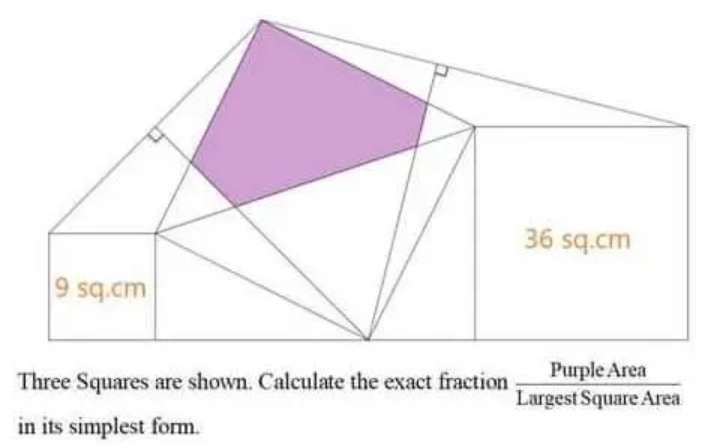
Sir Mike Ambrose is the author of the question.
Area largest square is;
(3√(5))²
= 45 cm²
Area purple is;
Area triangle with height equal base equal 3√(5) cm - area triangle with side 2....
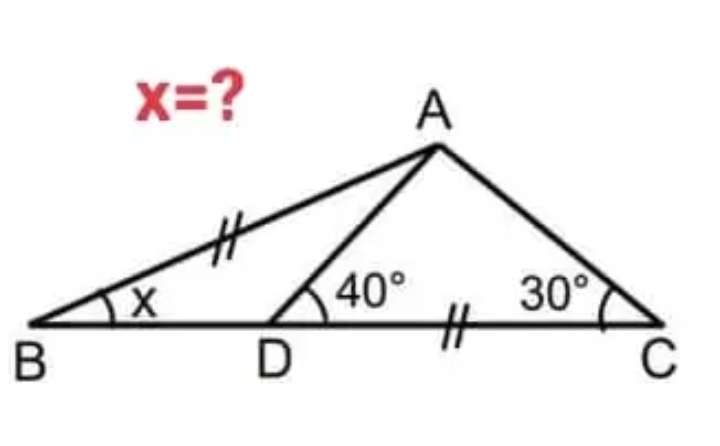
Let AB = CD = 1 unit.
a = 180-40-30
a = 110°
a is angle CAD.
(1/sin110) = (b/sin40)
b = 0.6840402867 units.
b is AC.
Therefore, the required angle, x is;
(0.6840402867/sinx) = (1/si...
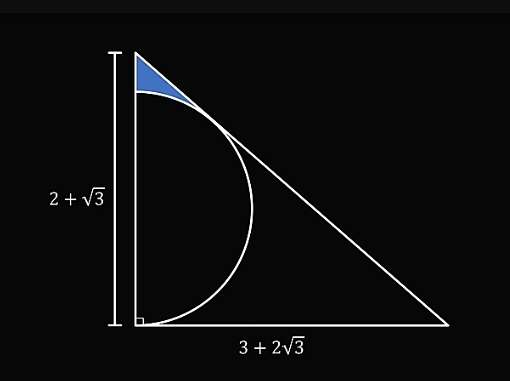
Calculating area shaded blue.
a² = (2+√(3))²+(3+2√(3))²
a² = 4+4√(3)+3+9+12√(3)+12
a² = 28+16√(3)
a = √(28+16√(3)) units.
a = 7.4641016151 units.
a is the hypotenuse of the ascribed right-a...
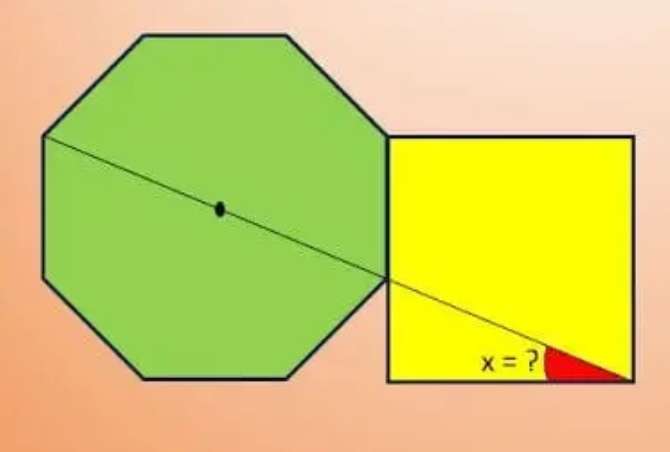
Let the side length of the regular octagon be 1 unit.
a = ⅛*180(8-2)
a = ⅛(180*6)
a = 135°
a is the single interior angle of the regular octagon.
2b² = 1²
b² = ½
b = ½√(2) units.
c =...
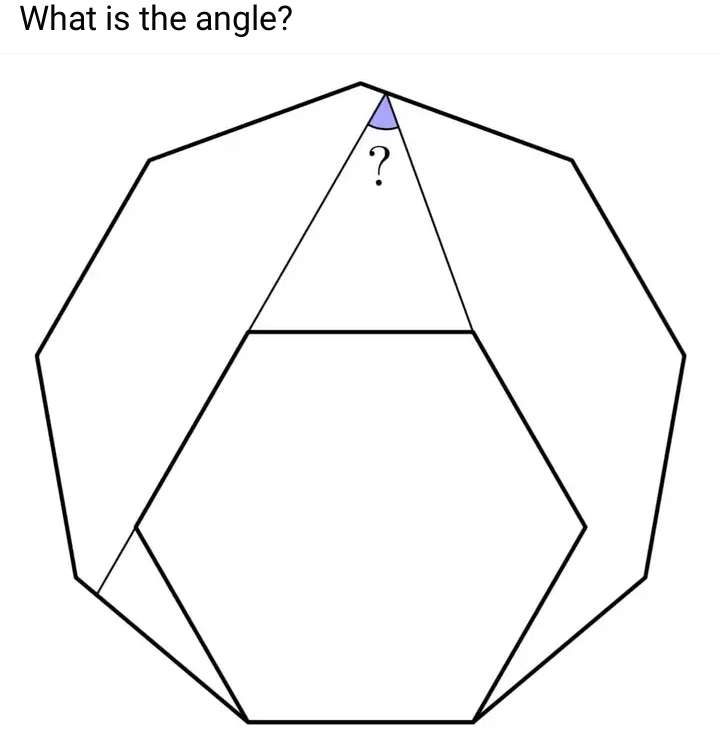
Let the side length of the inscribed regular hexagon which is equal the side length of the ascribed regular nonagon be 1 unit.
a = ⅙*180(6-2)
a = 120°
a is the single interior angle of the ins...
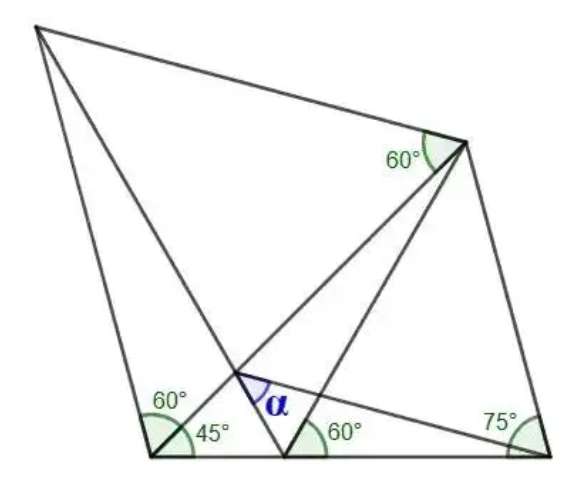
a = 180-45-75
a = 60°
b = 180-75-60
b = 45°
c = a-b
c = 15°
d = 180-60-45-c
d = 60°
e = 180-45-d
e = 75°
Therefore, the required angle, alpha, let it be f, is;
f = 180-d-e
f...
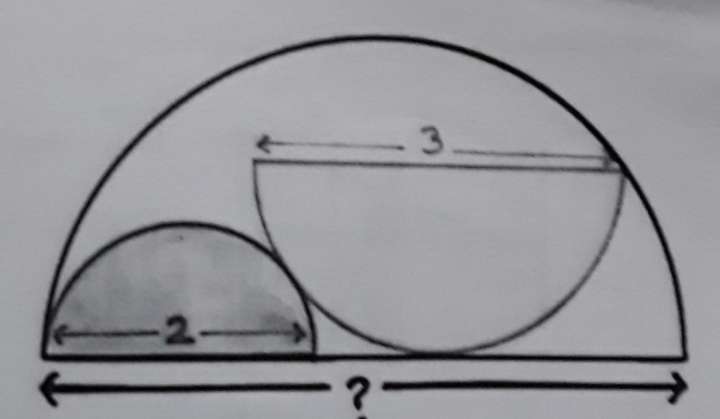
a = 1+1.5
a = 2.5 units.
b²+1.5² = 2.5²
b² = 6.25-2.25
b = √(4)
b = 2 units.
Let c be the radius of the ascribed semi circle.
d = 1+2
d = 3 units.
e = (3-c) units.
f = 1.5+e
f =...